题目内容
设 、
、 、
、 为同平面内具有相同起点的任意三个非零向量,且满足
为同平面内具有相同起点的任意三个非零向量,且满足 与
与 不共线,
不共线, ,
, ,则
,则 的值一定等于( )
的值一定等于( )
A.以 、 、 为两边的三角形面积; 为两边的三角形面积; | B.以 、 、 为邻边的平行四边形的面积; 为邻边的平行四边形的面积; |
C.以 、 、 为两边的三角形面积; 为两边的三角形面积; | D.以 、 、 为邻边的平行四边形的面积. 为邻边的平行四边形的面积. |
B
解析试题分析:由题意可以画出图形:记 ,记
,记

因为这三向量的起点相同,且满足 与
与 不共线,
不共线, ,
, ,
,
所以,由平面向量数量积的定义, =||OB||OC|cos
=||OB||OC|cos |,
|,
又由于S△BOC=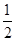 |OB||OC|sin
|OB||OC|sin ,所以||OB||OC|sin
,所以||OB||OC|sin |=S四边形OBDC.故选B.
|=S四边形OBDC.故选B.
考点:本题主要考查平面向量的数量积,平面向量在几何中的应用。
点评:中档题,利用数形结合思想,根据平面向量数量积的定义,确定得到平行四边形面积表达式。

练习册系列答案
相关题目
若 是非零向量且满足
是非零向量且满足 ,
, ,则
,则 与
与 的夹角是
的夹角是
A. | B. | C. | D. |
已知 为平面上不共线的三点,
为平面上不共线的三点, 是△ABC的垂心,动点
是△ABC的垂心,动点 满足
满足 ,则点
,则点 一定为△ABC的( )
一定为△ABC的( )
A. 边中线的中点 边中线的中点 | B. 边中线的三等分点(非重心) 边中线的三等分点(非重心) |
| C.重心 | D. 边的中点 边的中点 |
在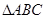 中,已知
中,已知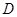 是
是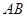 边上一点,若
边上一点,若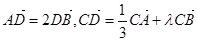 ,则
,则 等于
等于
A.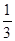 | B.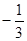 | C.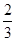 | D.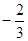 |
已知向量 ,
, 夹角为
夹角为 ,且|
,且| |=1,|
|=1,| |=
|= ,则|
,则| |等于( )
|等于( )
A. | B. | C. | D. |
已知不共线向量 则
则
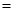
A. | B. | C. | D. |
已知△ABC, , 则△ABC的面积为( )
, 则△ABC的面积为( )
| A.1 | B.2 | C.3 | D.4 |
已知向量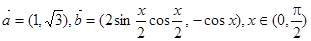 ,若
,若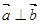 ,则
,则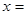
A.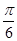 | B.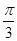 | C.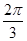 | D.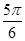 |
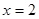 与双曲线
与双曲线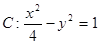 的渐近线交于
的渐近线交于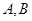 两点,设
两点,设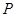 为双曲线
为双曲线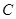 上的任意一点,若
上的任意一点,若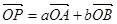 (
(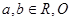 为坐标原点),则下列不等式恒成立的是( )
为坐标原点),则下列不等式恒成立的是( )