题目内容
11.已知函数f(x)=|x-a|,g(x)=x2+2ax+1(a为正常数),且函数f(x)和g(x)的图象与y轴相交于同一点.(Ⅰ)求a的值;
(Ⅱ)求函数f(x)+g(x)在[1,2]上的最大值与最小值.
分析 (Ⅰ)由题意知f(0)=g(0),从而解得;
(Ⅱ)令h(x)=f(x)+g(x)=|x-1|+x2+2x+1=x2+3x=(x+$\frac{3}{2}$)2-$\frac{9}{4}$,从而求最值.
解答 解:(Ⅰ)函数f(x)和g(x)的图象与y轴相交于同一点,
f(0)=g(0),
解得a=1.
(Ⅱ)令h(x)=f(x)+g(x)
=|x-1|+x2+2x+1,
∵x∈[1,2],
∴h(x)=f(x)+g(x)
=x-1+x2+2x+1
=x2+3x=(x+$\frac{3}{2}$)2-$\frac{9}{4}$,
h(x)的对称轴为x=-$\frac{3}{2}$,
当x∈[1,2]时,h(x)单调递增,
故hmin(x)=h(1)=4,hmax(x)=h(2)=10.
点评 本题考查了学生的化简运算能力及二次函数的性质应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.某几何体的三视图如图所示,则该几何体的表面积为( )
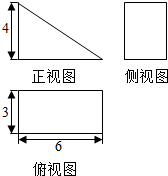

| A. | 36 | B. | $54+6\sqrt{13}$ | C. | $54+12\sqrt{5}$ | D. | $30+6\sqrt{73}$ |
19.设△ABC的内角A,B,C的对边分别为a,b,c,且sinA:sinB:sinC=2:3:4,则cosC的值为( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
6.在△ABC中,角A,B,C所对的边分别为a,b,c,且c=1,∠A=45°,S△ABC=2,则a=( )
| A. | 5 | B. | 25 | C. | $\sqrt{41}$ | D. | $5\sqrt{2}$ |
16.已知某三棱锥的三视图尺寸(单位cm)如图,则这个三棱锥的体积是( )


| A. | $\frac{8}{3}c{m^3}$ | B. | $\frac{4}{3}c{m^3}$ | C. | $\frac{2}{3}c{m^3}$ | D. | $\frac{1}{3}c{m^3}$ |
20.两平行线上分别有3个点、4个点,每两点确定一条直线,可以确定的直线的条数是( )
| A. | 12 | B. | 14 | C. | 15 | D. | 28 |
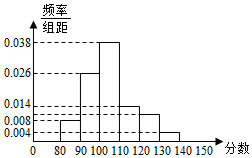 某中学一名高三数学教师,对其所教的文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)
某中学一名高三数学教师,对其所教的文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)