题目内容
y=sin(2x-
)-cos2x的图象可由y=
sin2x图象( )
| π |
| 6 |
| 3 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:y=sin(2x-
)-cos2x即y=
sin2(x-
),再利用函数y=Asin(ωx+φ)的图象变换规律得出结论.
| π |
| 6 |
| 3 |
| π |
| 6 |
解答:
解:∵y=sin(2x-
)-cos2x=
sin2x-
cos2x-cos2x=
(
sin2x-
cos2x)
=
sin(2x-
)=
sin2(x-
),
∴把y=
sin2x图象向右平移
个单位长度可得y=
sin2(x-
)的图象,
故选:C.
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=
| 3 |
| π |
| 3 |
| 3 |
| π |
| 6 |
∴把y=
| 3 |
| π |
| 6 |
| 3 |
| π |
| 6 |
故选:C.
点评:本题主要考查两角和差的正弦公式的应用,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.

练习册系列答案
相关题目
从集合{2,3,4,
,
}中取两个不同的数a,b,则logab>0的概率为( )
| 1 |
| 2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设命题p:?x0>0,使x02+2x0+a=0(a为实常数),则¬p为假命题的一个充分不必要条件是( )
| A、a<0 | B、a≤-1 |
| C、a<l | D、a>-2 |
阅读程序框图,若输出的函数值在区间[0,4]上,则输入的实数x的取值范围是( )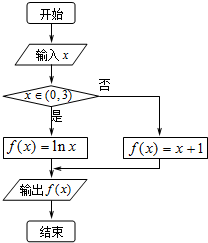

| A、{x∈R|-1≤x≤0或1≤x≤3} |
| B、{x∈R|-1≤x≤0或1≤x<3} |
| C、{x∈R|-1≤x≤0或1≤x≤e4} |
| D、{x∈R|-1≤x≤3} |
设函数f(x)=3sin(2x+
)+1,将y=f(x)的图象向右平移φ(φ>0)个单位,使得到的图象关于y轴对称,则φ的最小值为( )
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 三棱锥P-ABC的三视图如图所示,其中P是直角顶点.设M是面ABC内一点.定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(6,x,y),且
三棱锥P-ABC的三视图如图所示,其中P是直角顶点.设M是面ABC内一点.定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(6,x,y),且