题目内容
20.函数$y=cos(\frac{π}{6}+2x)$单调递减区间为[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z.分析 利用余弦函数的单调性,求得函数$y=cos(\frac{π}{6}+2x)$单调递减区间.
解答 解:对于函数$y=cos(\frac{π}{6}+2x)$,令2kπ≤2x+$\frac{π}{6}$≤2kπ+π,求得kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$,
可得函数的减区间为[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z,
故答案为:[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z.
点评 本题主要考查余弦函数的单调性,属于基础题.

练习册系列答案
相关题目
11.已知集合A={x||x-1|<2},B={x|-1<x<m+1},若x∈A成立的一个必要不充分条件是x∈B,则实数m的取值范围是( )
| A. | [2,+∞) | B. | (-∞,2] | C. | (2,+∞) | D. | (-∞,2) |
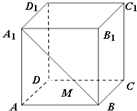 如图,棱长为1的正方体ABCD-A1B1C1D1中,M为线段A1B上的动点,则下列结论正确的有①②
如图,棱长为1的正方体ABCD-A1B1C1D1中,M为线段A1B上的动点,则下列结论正确的有①②