题目内容

10．已知E，F，G，H为空间四边形ABCD的边AB，BC，CD，DA上的中点，且异面直线AC与BD所成的角为450，AC=6，BD=4．求四边形EFGH的面积．

分析 连接HG、GF、FE、EH，则HG∥AC∥EF，HE∥BD∥GF，由此能证明四边形EFGH为平行四边形，且HE=2  EF=3，又所给条件得∠HEF=135°或45°，即可得出结论．

解答 解：分别连接HG、GF、FE、EH，则HG∥AC∥EF，HE∥BD∥GF，
可得四边形EFGH为平行四边形，且HE=2  EF=3，
又所给条件得∠HEF=135°或45°
由面积公式可得四边形EFGH的面积为3$\sqrt{2}$

点评 本题考查四边形为平行四边形的证明，考查四边形EFGH的面积的求法，是中档题．

练习册系列答案
相关题目
12．在正项数列{an}中，an+12=anan+2（?n∈N*），已知a1=$\frac{1}{4}$，a8=8a5
（1）求数列{an}的通项公式；
（2）若数列{bn}满足bn=log2an，数列{bn}的前n项和为Sn，求数列{$\frac{{S}_{n}+\frac{5n}{2}+8}{n}$}的最小项及其值．
13．在平面直角坐标系xOy中，设A，B，C是圆x2+y2=1上相异三点，若存在正实数λ，? 使得 $\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$，则λ2+（?-3）2的取值范围是（　　）
A．[0，+∞）B．（2，+∞）C．（2，8）D．（8，+∞）
10．在直角坐标系xOy中，圆C的方程为（x-1）2+y2=$\frac{1}{2}$，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，点M的极坐标为（2，θ），过点M斜率为1的直线交圆C于A，B两点．
（1）求圆C的极坐标方程；
（2）求|MA|•|MB|的范围．
5．已知△ABC的外接圆半径为8，且sinA：sinB：sinC=2：3：4，则△ABC的面积为$\frac{45\sqrt{15}}{4}$．
15．（1）当x∈[$\frac{π}{6}$，$\frac{7π}{6}$]时，求函数y=3-sin x-2cos2x的最大值．
（2）已知5sinβ=sin（2α+β），tan（α+β）=$\frac{9}{4}$，求tanα
2．如图，∠ACB=90°，CD⊥AB于D，AD=3，CD=2，则$\frac{AC}{BC}$的值为（　　）
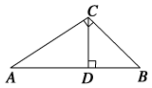
A．$\frac{3}{2}$B．$\frac{9}{4}$C．$\frac{2}{3}$D．$\frac{4}{9}$
19．若集合A∪B=B∩C，则集合A，B，C的关系下列表示正确的是（　　）
A．A⊆B⊆CB．C⊆B⊆AC．B⊆C⊆AD．B⊆A⊆C
20．函数$y=cos（\frac{π}{6}+2x）$单调递减区间为[kπ-$\frac{π}{12}$，kπ+$\frac{5π}{12}$]，k∈Z．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网