题目内容
1．
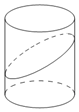一个底面半径为2的圆柱被与其底面所成角是60°的平面所截，截面是一个椭圆，则该椭圆的焦距等于$4\sqrt{3}$．
分析 利用已知条件，求出题意的长半轴，短半轴，然后求出半焦距，即可．
解答 解：因为底面半径为R的圆柱被与底面成30°的平面所截，其截口是一个椭圆，
则这个椭圆的短半轴为：R，长轴为：$\frac{2R}{cos60°}$=8，
∵a2=b2+c2，∴c=$\sqrt{16-4}$=2$\sqrt{3}$，
∴椭圆的焦距为$4\sqrt{3}$；
故答案为：4$\sqrt{3}$．
点评 本题考查椭圆焦距的求法，注意椭圆的几何量关系的正确应用，考查计算能力．
练习册系列答案
相关题目
6．已知函数$f（x）=sin（2x+\frac{π}{3}）$在区间[0，a]（其中a＞0）上单调递增，则实数a的取值范围是（ ）
| A． | $0＜a≤\frac{π}{2}$ | B． | $0＜a≤\frac{π}{12}$ | ||
| C． | $a=kπ+\frac{π}{12}，k∈{N^*}$ | D． | $2kπ＜a≤2kπ+\frac{π}{12}，k∈N$ |