题目内容
19.设x,y∈R,向量$\overrightarrow a=(x,1)$,$\overrightarrow b=(1,y)$,$\overrightarrow c=(2,-4)$且$\overrightarrow a⊥\overrightarrow c$,$\overrightarrow b∥\overrightarrow c$,则x+y=0.分析 利用向量共线定理、向量垂直与数量积的共线即可得出.
解答 解:∵$\overrightarrow a⊥\overrightarrow c$,$\overrightarrow b∥\overrightarrow c$,
∴$\overrightarrow{a}•\overrightarrow{c}$=2x-4=0,2y+4=0,
则x=2,y=-2.
∴x+y=0.
故答案为:0.
点评 本题考查了向量共线定理、向量垂直与数量积的共线,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
4.在下列各区间中,存在着函数f(x)=x3+4x-3的零点的区间是( )
| A. | [-1,0] | B. | [0,1] | C. | [1,2] | D. | [2,3] |
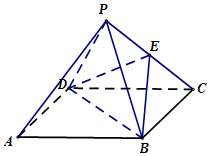 如图,在正四棱锥P-ABCD中,PA=AB=a,E是棱PC的中点.
如图,在正四棱锥P-ABCD中,PA=AB=a,E是棱PC的中点.