题目内容
【题目】在直角坐标系
中，曲线
的参数方程为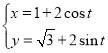
（
为参数），以坐标原点为极点，
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为
，且曲线关于直线对称．
（1）求
；
（2）若直线与曲线交于
，
，直线
：
与曲线交于，
，且
的面积不超过
，求直线的倾斜角的取值范围．
【答案】（1）
；（2）
．
【解析】
（1）把参数方程化为圆的方程，根据圆关于直线对称，易知直线过圆心，代入即可得解；
（2）若设直线
：
，代入圆的极坐标方程，再利用面积公式即可得解，或者再利用直线和圆的普通方法即可得解.
【解】（1）消参可得曲线
的普通方程：
，即以
为圆心，半径为2的圆，
依题知直线
过圆心，．
（2）【法一】将化为极坐标方程：
，直线：，
，
依题：
，
，又
，
可得：
，
又
，
不重合，可得：
，综上，
的范围为．
【法二】
如图，设
，
，
，
，
，
，
得：
，
又，不重合，可得：，综上，的范围为．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
