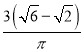题目内容
【题目】已知点F1为椭圆![]() 的左焦点,
的左焦点,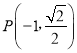 在椭圆上,PF1⊥x轴.
在椭圆上,PF1⊥x轴.
(1)求椭圆的方程:
(2)已知直线l与椭圆交于A,B两点,且坐标原点O到直线l的距离为![]() 的大小是否为定值?若是,求出该定值:若不是,请说明理由.
的大小是否为定值?若是,求出该定值:若不是,请说明理由.
【答案】(1)![]() y2=1;(2)∠AOB为定值
y2=1;(2)∠AOB为定值![]()
【解析】
(1)由PF1⊥x轴,及点P的坐标可得F1的坐标,即c的值,将P的坐标代入,由a,b,c之间的关系的关系求出a,b的值,进而求出椭圆的方程;
(2)分直线l的斜率存在和不存在两种情况讨论:当斜率不存在时由原点到直线的距离可得直线l的方程,代入椭圆中求出A,B的坐标,进而可得数量积![]() 的值为0,可得∠AOB
的值为0,可得∠AOB![]() ;当直线l的斜率存在时,设直线l的方程与椭圆联立求出两根之和及两根之积,由原点到直线的距离可得参数之间的关系,将其代入数量积
;当直线l的斜率存在时,设直线l的方程与椭圆联立求出两根之和及两根之积,由原点到直线的距离可得参数之间的关系,将其代入数量积![]() 的表达式,可得恒为0,即∠AOB恒为定值
的表达式,可得恒为0,即∠AOB恒为定值![]()
(1)因为PF1⊥x轴,又 在椭圆上,可得F1(﹣1,0),
在椭圆上,可得F1(﹣1,0),
所以c=1,![]() 1,a2=c2+b2,
1,a2=c2+b2,
解得a2=2,b2=1,
所以椭圆的方程为:![]() y2=1;
y2=1;
(2)当直线l的斜率不存在时,由原点O到直线l的距离为![]() ,
,
可得直线l的方程为:x![]() ,
,
代入椭圆可得A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() )或A(
)或A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
可得![]() ,所以∠AOB
,所以∠AOB![]() ;
;
当直线l的斜率存在时,设直线的方程为:y=kx+m,设A(x1,y1),B(x2,y2),
由原点O到直线l的距离为![]() ,可得
,可得 ,可得3m2=2(1+k2),①
,可得3m2=2(1+k2),①
直线与椭圆联立 ,整理可得(1+2k2)x2+4kmx+2m2﹣2=0,
,整理可得(1+2k2)x2+4kmx+2m2﹣2=0,
![]() =16k2m2﹣4(1+2k2)(2m2﹣2)>0,将①代入
=16k2m2﹣4(1+2k2)(2m2﹣2)>0,将①代入![]() 中可得
中可得![]() =16m2+8>0,
=16m2+8>0,
x1+x2![]() ,x1x2
,x1x2![]() ,
,
y1y2=k2x1x2+km(x1+x2)+m2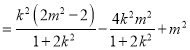
![]() ,
,
所以![]()
![]() ,
,
将①代入可得![]() 0,
0,
所以∠AOB![]() ;
;
综上所述∠AOB![]() 恒成立.
恒成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目