题目内容
设函数 ,
,
(I)求函数 在
在 上的最大值与最小值;
上的最大值与最小值;
(II)若实数 使得
使得 对任意
对任意 恒成立,求
恒成立,求 的值.
的值.
(I)最大值为3,最小值为2(II)-1
解析试题分析:(I)将函数 化为
化为 ,再求出最值;
,再求出最值;
(II)由 和
和 求出a、b、c,再将值代入
求出a、b、c,再将值代入 。
。
解:(I)由条件知 ,
,
由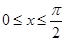 知,
知,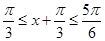 ,于是
,于是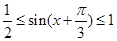
所以 时,
时, 有最小值
有最小值 ;
;
当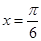 时,
时, 有最大值
有最大值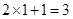 .
.
(II)由条件可知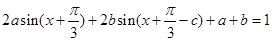 对任意的
对任意的 恒成立,
恒成立,
∴
∴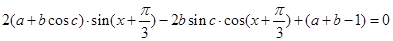
∴ 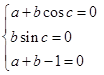 ,
,
由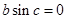 知
知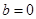 或
或 .
.
若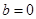 时,则由
时,则由 知
知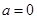 ,这与
,这与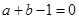 矛盾!
矛盾!
若 ,则
,则 (舍去),
(舍去), ,
,
解得 ,所以,
,所以,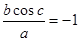
考点:三角函数的最值.
点评:本题主要考查两角和与差的正弦公式和正弦函数的性质:单调性、最值.考查考生对基础知识的掌握程度和熟练应用程度.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
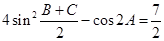 .
.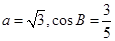 ,求△ABC的面积.
,求△ABC的面积.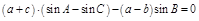 ,其中
,其中 、
、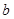 、
、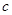 分别为
分别为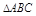 的内角
的内角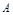 、
、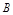 、
、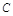 所对的边.求:
所对的边.求: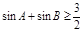 的角
的角 (
(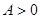 ,
,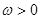 ,
,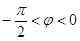 )的图像与
)的图像与 轴的交点
轴的交点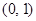 ,它在
,它在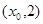 和
和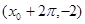
 的解析式;
的解析式;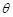 满足
满足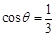 ,求
,求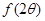 的值.
的值.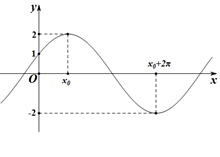
 cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为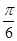 .
.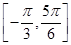 上的最小值为
上的最小值为 , 分别设
, 分别设 的面积为
的面积为 .
.
 表示
表示 的最大值及取最大值时
的最大值及取最大值时 的值.
的值. =
= .
.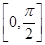 上的最大值和最小值.
上的最大值和最小值. 的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记
的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记 ,求当角
,求当角 取何值时, 矩形ABCD的面积最大?并求出这个最大值.
取何值时, 矩形ABCD的面积最大?并求出这个最大值.
 为第三象限角,
为第三象限角, .
. ;
;  ,求
,求