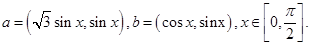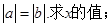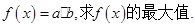题目内容
如图,已知OPQ是半径为1，圆心角为
的扇形，C是扇形弧上的动点,ABCD是扇形的内接矩形,记
,求当角
取何值时, 矩形ABCD的面积最大?并求出这个最大值.
= 
矩形ABCD面积的最大值为
。
解析试题分析：解：由题意可得
在三角形OCB中，OC=1,
,
所以 BC=sin OB=cos
在三角形OAD中，
，AD="BC=" sin
所以 
所以AB="OB-OA=" cos - 
5分
则，矩形ABCD的面积为
= 
=
=
所以矩形ABCD面积的最大值为。
此时
=
= 12分
考点：三角函数的运用
点评：主要是考查了三角函数的实际问题中的运用，属于中档题。
练习册系列答案
全能测控期末小状元系列答案
相关题目
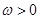，函数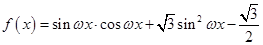
的最小正周期为
.
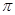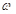的值；
在区间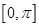
上的图象，并根据图象写出其在区间
，
在
上的最大值与最小值；
使得
对任意
恒成立，求
的值．
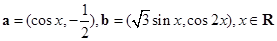, 设函数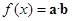
. 
上的最大值和最小值. 
.
的最小正周期及单调递增区间； 
，求
的值. 
的图像经过怎样的变换得到. 
的图象过点(1,2)，相邻两条对称轴间的距离为2，且
的最大值为2.
； 
；
在区间[1，4]上恰有一个零点，求
的范围.
（
），该函数所表示的曲线上的一个最高点为
，由此最高点到相邻的最低点间曲线与x轴交于点（6，0）。
函数解析式；
，求
