题目内容
15.已知函数$f(x)=2ln(x+1)+\frac{1}{2}m{x^2}-(2m+1)x$(Ⅰ)若x=1是f(x)的极值点,求f(x)的极值;
(Ⅱ)若f(x)有两个极值点,求m的取值范围.
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(Ⅱ)求出函数的导数,通过讨论m的范围,求出函数的单调区间,根据函数的极值点的个数,确定m的范围即可.
解答 解:(Ⅰ)f′(x)=$\frac{2}{x+1}$+mx-(2m+1),
由已知得,f′(1)=1-m=0,m=1,
此时f′(x)=$\frac{(x-1)(x-2)}{x}$,
由f′(x)=0,得x=1或x=2,
随x的变化f′(x)、f(x)的变化情况如下:
| x | (0,1) | 1 | (1,2) | 2 | (2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
(Ⅱ)f(x)定义域为(0,+∞),
f′(x)=$\frac{(mx-1)(x-2)}{x+1}$,
(1)当m=0时,f′(x)=$\frac{-x+2}{x+1}$,
x∈(0,2),f′(x)>0,x∈(2,+∞),f′(x)<0,
所以x=2时,f(x)取得极大值;
(2)当m≠0时,由f′(x)=0,得x=2或x=$\frac{1}{m}$,
①若m<0,则$\frac{1}{m}$<0,x∈(0,2),f′(x)>0,x∈(2,+∞),f′(x)<0,
所以x=2时,f(x)取得极大值;
②若m=$\frac{1}{2}$,则$\frac{1}{m}$=2,f′(x)=$\frac{{(x-2)}^{2}}{2x}$≥0,
f(x)在(0,+∞)上为增函数,无极值;
③若0<m<$\frac{1}{2}$,则$\frac{1}{m}$>2,随x的变化f′(x)、f(x)的变化情况如下:
| x | (0,2) | 2 | (2,$\frac{1}{m}$) | $\frac{1}{m}$ | ($\frac{1}{m}$,+∞) |
| f′(x)) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
④若m>$\frac{1}{2}$,则0<$\frac{1}{m}$<,随x的变化f′(x),f(x)的变化情况如下:
| x | (0,$\frac{1}{m}$) | $\frac{1}{m}$ | ($\frac{1}{m}$,2) | 2 | (2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
综上:f(x)有两个极值点,m的取值范围是(0,$\frac{1}{2}$)∪($\frac{1}{2}$,+∞).
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,是一道综合题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
3.已知$f(x)=\frac{lnx}{x}$,则( )
| A. | f(2)>f(e)>f(3) | B. | f(3)>f(e)>f(2) | C. | f(3)>f(2)>f(e) | D. | f(e)>f(3)>f(2) |
20.要测量电视塔AB的高度,在C点测得塔顶的仰角是45°,在D点测得塔顶的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度是( )
| A. | 30m | B. | 40m | C. | $40\sqrt{3}$m | D. | $40\sqrt{2}$m |
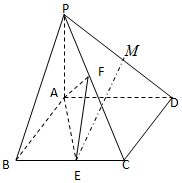 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,E是BC中点,M是PD上的中点,F是PC上的动点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,E是BC中点,M是PD上的中点,F是PC上的动点.