题目内容
12.“a+b=1”是“直线x+y+1=0与圆(x-a)2+(y-b)2=2相切”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由直线x+y+1=0与圆(x-a)2+(y-b)2=2相切可得,从而可得a,b之间的关系,即可作出判断
解答 解:直线x+y+1=0与圆(x-a)2+(y-b)2=2相切
∴$\frac{|a+b+1|}{\sqrt{2}}$=$\sqrt{2}$,
∴|a+b+1|=2,
∴a+b=1或a+b=-3,
∴“a+b=1”是“直线x+y+1=0与圆(x-a)2+(y-b)2=2相切”的充分不必要条件,
故选:A
点评 本题以充分与必要条件的判断为载体,主要考查了直线与圆相切的性质的应用.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
3.已知$f(x)=\left\{\begin{array}{l}1+x,x∈R\\(1+i)x,x∉R\end{array}\right.$,则f[f(1-i)]等于( )
| A. | 3 | B. | 1 | C. | 2-i | D. | 3+i |
20.执行如图所示的程序框图,如果输入N=30,则输出S=( )
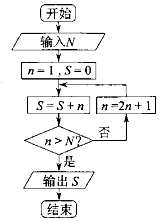

| A. | 26 | B. | 57 | C. | 225 | D. | 256 |
7.某校开展“翻转合作学习法”教学实验,经过一年的实践后,对“翻转班”和“对照班”的全部220名学生的数学学习情况进行测试,按照大于或等于120分为“成绩优秀”,120分以下为“成绩一般”统计,得到如下的2×2列联表.
(Ⅰ)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关;
(Ⅱ)为了交流学习方法,从这次测试数学成绩优秀的学生中,用分层抽样方法抽出6名学生,再从这6名学生中抽3名出来交流学习方法,求至少抽到一名“对照班”学生交流的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$:
| 成绩优秀 | 成绩一般 | 合计 | |
| 对照班 | 20 | 90 | 110 |
| 翻转班 | 40 | 70 | 110 |
| 合计 | 60 | 160 | 220 |
(Ⅱ)为了交流学习方法,从这次测试数学成绩优秀的学生中,用分层抽样方法抽出6名学生,再从这6名学生中抽3名出来交流学习方法,求至少抽到一名“对照班”学生交流的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
4.已知集合S={1,2},设S的真子集有m个,则m=( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
1.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,双曲线 x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为8,则椭圆C的方程为( )
| A. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{5}$=1 |