题目内容
抛物线:y2=2px(p>0),倾斜角为45°的弦AB的中点为M
(1)若M=(m,2)求抛物线方程;
(2)若以AB为直径的圆过原点,求实数M的横坐标.
(1)若M=(m,2)求抛物线方程;
(2)若以AB为直径的圆过原点,求实数M的横坐标.
考点:抛物线的标准方程,圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)设出弦所在直线方程,和抛物线方程联立后化为关于y的一元二次方程,然后利用根与系数关系求解;
(2)由以AB为直径的圆过原点得到
•
=0,转化为坐标运算求得直线的截距,再由中点坐标公式求得M的横坐标.
(2)由以AB为直径的圆过原点得到
| OA |
| OB |
解答:
解:(1)设弦所在直线方程为y=x+b,
联立
,得y2-2py+2pb=0,
∵M(m,2)为弦的中点,
∴y1+y2=2p=4,p=2.
∴抛物线方程为y2=4x;
(2)设A(x1,y1),B(x2,y2),
由(1)知,y1+y2=4,y1y2=4b,
则x1x2=(y1-b)(y2-b)=y1y2-b(y1+y2)+b2
=4b-4b+b2=b2.
∵以AB为直径的圆过原点,
∴
•
=0,即x1x2+y1y2=b2+4b=0,
解得:b=0或b=-4,
m=
=
-b=2-b.
当b=0时,m=2;
当b=-4时,m=6.
联立
|
∵M(m,2)为弦的中点,
∴y1+y2=2p=4,p=2.
∴抛物线方程为y2=4x;
(2)设A(x1,y1),B(x2,y2),
由(1)知,y1+y2=4,y1y2=4b,
则x1x2=(y1-b)(y2-b)=y1y2-b(y1+y2)+b2
=4b-4b+b2=b2.
∵以AB为直径的圆过原点,
∴
| OA |
| OB |
解得:b=0或b=-4,
m=
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
当b=0时,m=2;
当b=-4时,m=6.
点评:本题考查了抛物线方程的求法,考查了直线与抛物线的关系,涉及直线与圆锥曲线关系问题,常采用联立直线与圆锥曲线方程,化为关于x的一元二次方程后利用根与系数关系求解,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2x3-x2-2x+1=0的三个根分别是α,β,γ,则α+β+γ+αβγ的值为( )
| A、-1 | ||
| B、0 | ||
C、-
| ||
D、
|
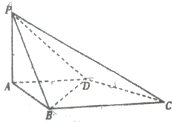 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AD=AB=1.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AD=AB=1.