题目内容
已知α，β均为锐角，且sinβ=
，cosα=
，求α-β的值．
| ||
| 5 |
| ||
| 10 |
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：由角的范围和同角三角函数的基本关系可得sinα和cosβ，代入两角差的余弦公式可得余弦值，结合角的范围可得．
解答：
解：∵α，β均为锐角，且sinβ=
，cosα=
，
∴sinα=
=
，
∴cosβ=
=
，
又sinβ=
＜sinα=
，
∴β＜α，∴0＜α-β＜
，
∴cos（α-β）=cosαcosβ+sinαsinβ=
，
∴α-β=
．
| ||
| 5 |
| ||
| 10 |
∴sinα=
| 1-cos2α |
3
| ||
| 10 |
∴cosβ=
| 1-sin2β |
2
| ||
| 5 |
又sinβ=
| ||
| 5 |
3
| ||
| 10 |
∴β＜α，∴0＜α-β＜
| π |
| 2 |
∴cos（α-β）=cosαcosβ+sinαsinβ=
| ||
| 2 |
∴α-β=
| π |
| 4 |
点评：本题考查两角和与差的三角函数公式，涉及同角三角函数的基本关系，属基础题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
已知圆（x-2）2+（y-2）2=1的圆心为M，由直线x+y+a=0上任意一点P引圆的一条切线，切点为A，若
•
＞1恒成立，则实数a的取值范围为（ ）
| PM |
| PA |
| A、（-∞，-6）∪（-2，+∞） |
| B、（-∞，-6]∪[-2，+∞） |
| C、（-6，-2） |
| D、[-6，-2] |
已知函数f（x）在R上可导，其导函数为f′（x），且函数F（x）=（1-x）f′（x）的图象如图所示，零点分别为-1，1，2，则f（-1），f（1），f（2）的大小关系正确的是（ ）| A、f（-1）=f（1）=f（2） |
| B、f（-1）＜f（1）＜f（2） |
| C、f（-1）＞f（1）＞f（2） |
| D、f（-1）＜f（2）＜f（1） |
已知一次函数y=kx+b的图象如图所示，则k，b的符号是（ ）
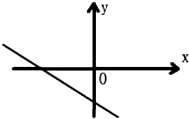
| A、k＞0，b＞0 |
| B、k＞0，b＜0 |
| C、k＜0，b＞0 |
| D、k＜0，b＜0 |