题目内容
设函数ex|lnx|=1两个不同的实根为x1，x2，则（ ）
| A、x1x2＜0 |
| B、x1x2=1 |
| C、0＜x1x2＜1 |
| D、x1x2＞1 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：由题意f（x）=e-x-|lnx|的零点，即方程e-x=|lnx|的实数根．因此在同一坐标系内作出函数y=e-x与y=|lnx|的图象，并设
x1＜x2，可得lnx2＜-lnx1，推出x1x2＜1．再根据x1＞
且x2＞1得到x1x2＞
，由此即可得到本题的答案．
x1＜x2，可得lnx2＜-lnx1，推出x1x2＜1．再根据x1＞
| 1 |
| e |
| 1 |
| e |
解答：
解：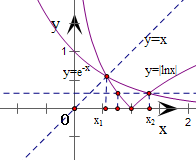
函数f（x）=e-x-|lnx|的零点，即方程e-x=|lnx|的实数根
同一坐标系内作出函数y=e-x与y=|lnx|的图象，如图所示
不妨设x1＜x2，可得0＜x1＜1且x2＞1
∵0＜-lnx1＜1，∴lnx1＞-1，可得x1＞
∵x2＞1，∴x1x2＞
又∵y=e-x是减函数，可得lnx2＜-lnx1，
∴lnx2+lnx1＜0，得lnx1x2＜0，即x1x2＜1
综上所述，可得
＜x1x2＜1
故选：C
函数f（x）=e-x-|lnx|的零点，即方程e-x=|lnx|的实数根同一坐标系内作出函数y=e-x与y=|lnx|的图象，如图所示
不妨设x1＜x2，可得0＜x1＜1且x2＞1
∵0＜-lnx1＜1，∴lnx1＞-1，可得x1＞
| 1 |
| e |
∵x2＞1，∴x1x2＞
| 1 |
| e |
又∵y=e-x是减函数，可得lnx2＜-lnx1，
∴lnx2+lnx1＜0，得lnx1x2＜0，即x1x2＜1
综上所述，可得
| 1 |
| e |
故选：C
点评：本题给出含有指数和对数的基本初等函数，求函数的两个零点满足的条件，着重考查了指数函数、对数函数的图象与性质，以及函数的零点与方程根的关系等知识点，属于中档题．
练习册系列答案
相关题目
命题“x2-9=0的解是x=±3”，在这个命题中，使用的逻辑联结词的情况是（ ）
| A、没有使用逻辑联结词 |
| B、使用了“且” |
| C、使用了“或” |
| D、使用了“非” |
下列说法正确的是（ ）
| A、若p∧q为假命题，则p、q都为假命题 | ||||||||
| B、“f（0）=0”是“函数f（x）为奇函数”充要条件 | ||||||||
| C、若命题p：?x0∈R，2x02+x0+3＞0，则?p：?x∈R，2x2+x+3＜0 | ||||||||
D、若“a=
|
用数学归纳法证明等式（n+1）（n+2）×…×（n+n）=2n×1×3×…×（2n-1）的过程中，由n=k（k∈N*）推出n=k+1（k∈N*）成立时，左边应增加的因式是（ ）
| A、2k+1 | ||
| B、2（2k+1） | ||
C、
| ||
D、
|