题目内容
求证:双曲线
(a＞0,b＞0)上任何一点到两条渐近线的距离之积为定值.
证法一:设P(x0,y0)是双曲线上任意一点,
由双曲线的两条渐近线方程为bx+ay=0和bx-ay=0,
可得P到bx+ay=0的距离;
P到bx-ay=0的距离
.
∴
.
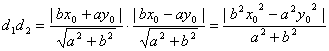又P在双曲线上,∴
,即b2x02-a2y02=a2b2.
∴
,即P到两条渐近线的距离之积为定值.
证法二:设双曲线上任一点P(asecθ,btanθ),
∵双曲线的两条渐近线方程为bx+ay=0和bx-ay=0.
∴点P到直线bx+ay=0的距离
.
点P到直线bx-ay=0的距离
.
∴
.
∴双曲线上任一点到两条渐近线的距离之积为定值.
启示:(1)所谓定值,是与P点在曲线上的位置无关,为了达到目标明确,可先通过特殊的情况,求出一个常数,猜想其定值.
(2)双曲线
(a＞0,b＞0)的参数方程为
(θ为参数),不作过高要求,在解题中灵活应用即可,类似于换元法解题,将可达到一元化的目的.
练习册系列答案
智能训练练测考系列答案
相关题目
，其中m、n∈R，且m-2n=1，
(a＞0，b＞0，且a≠b)交于两点M、N，且以MN为直径的圆过原点，求证
为定值；
，求双曲线实轴长的取值范围． 
(a＞0,b＞0)的焦点坐标是F1(-c,0)和F2(c,0),P(x0,y0)?是双曲线上的任一点,求证:|PF1|=|a+ex0|,|PF2|=|a-ex0|,其中e是双曲线的离心率.
(a＞0,b＞0)的一个焦点F作x轴的垂线,交双曲线的一支于P、Q两点,又过F作一直线平行于双曲线的一条渐近线,交双曲线于R,求证:|PQ|=4|FR|.
(a＞0,b＞0)上的任意一点,过P分别作双曲线的渐近线的平行线,分别与渐近线交于M、N两点,求证:|PM|·|PN|=
c2(c为双曲线的半焦距).