题目内容
过双曲线
证明:设F点的坐标为(c,0),
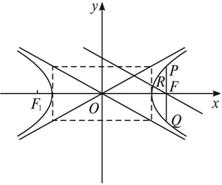
将x=c代入双曲线方程![]() ,
,
得![]() ,
,
∴![]() .
.
过点F(c,0),且与双曲线的渐近线bx+ay=0平行的直线为![]() ,
,
代入双曲线方程,得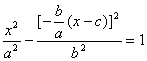 .
.
解之得![]() ,代入
,代入![]() ,
,
得![]() ,即
,即![]() .
.
∴|FR|2=(x-c)2+y2=(![]() -c)2+
-c)2+![]()
![]() .
.
故![]() ,∴|PQ|=4|FR|.
,∴|PQ|=4|FR|.
启示:欲证|PQ|等于4|FR|,只需用双曲线的基本量a、b表示它们.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
过双曲线
证明:设F点的坐标为(c,0),

将x=c代入双曲线方程![]() ,
,
得![]() ,
,
∴![]() .
.
过点F(c,0),且与双曲线的渐近线bx+ay=0平行的直线为![]() ,
,
代入双曲线方程,得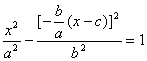 .
.
解之得![]() ,代入
,代入![]() ,
,
得![]() ,即
,即![]() .
.
∴|FR|2=(x-c)2+y2=(![]() -c)2+
-c)2+![]()
![]() .
.
故![]() ,∴|PQ|=4|FR|.
,∴|PQ|=4|FR|.
启示:欲证|PQ|等于4|FR|,只需用双曲线的基本量a、b表示它们.

 阅读快车系列答案
阅读快车系列答案