题目内容

15．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+b，x≤0}\\{lo{g}_{2}x，x＞0}\end{array}\right.$，若f[f（$\frac{1}{2}$）]=3，则b=（　　）
A．-1B．0C．2D．3

分析 利用分段函数的解析式，由里及外逐步求解函数值，列出方程求解即可．

解答 解：函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+b，x≤0}\\{lo{g}_{2}x，x＞0}\end{array}\right.$，
f（$\frac{1}{2}$）=log2$\frac{1}{2}$=-1，
f[f（$\frac{1}{2}$）]=3，可得f（-1）=1+b=3，可得b=2．
故选：C．

点评 本题考查分段函数的应用，函数值的求法，考查计算能力．

练习册系列答案
相关题目
5．已知直线x+ylog4a=0与直线2x-y-3=0平行，则a的值为（　　）
A．$\frac{1}{2}$B．2C．4D．16
6．我们知道：在平面内，点（x0，y0）到直线Ax+By+C=0的距离公式为$d=\frac{{|{A{x_0}+B{y_0}+C}|}}{{\sqrt{{A^2}+{B^2}}}}$，通过类比的方法，可求得：在空间中，点（2，4，1）到平面x+2y+2z+3=0的距离为5．
3．设向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=3，$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{2}$，|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\frac{3\sqrt{6}}{2}$，则向量$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为$\frac{\sqrt{6}}{2}$．
10．设抛物线y2=8x的焦点为F，过F作倾斜角为60°的直线交抛物线于A，B两点（点A在第一象限），与其准线交于点C，则$\frac{{S}_{△AOC}}{{S}_{△BOF}}$=（　　）
A．6B．7C．8D．10
20．设变量x，y满足约束条件$\left\{\begin{array}{l}2x+y≤2\\ x+y≥-1\\ y≤x\end{array}\right.$，则目标函数z=2x-y的最大值为10．
7．已知水池的长为30m，宽为20m，一海豚在水池中自由游戏，则海豚嘴尖离池边超过4m的概率为$\frac{11}{25}$．
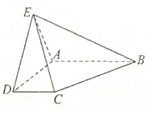4．如图，四棱锥E-ABCD中，底面ABCD为梯形，AB∥CD，且AB=2CD，侧面ADE为等边三角形，侧面ABE为等腰直角三角形，且角A为直角，且平面ABE⊥平面ADE．
（Ⅰ）证明：平面ABE⊥平面BCE；
（Ⅱ）求平面ADE和平面BCE所成二面角（锐角）的大小．
5．已知函数f（x）=2sin（2ωx+$\frac{π}{6}$）+1（其中0＜ω＜1），若点（-$\frac{π}{6}$，1）是函数f（x）图象的一个对称中心．
（Ⅰ）试求函数f（x）的解析式；
（Ⅱ）求函数f（x）在区间[-π，π]上的单调递减区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网