题目内容
1．
在正方形网格中，某四面体的三视图如图所示．如果小正方形网格的边长为1，那么该四面体最长棱的棱长为（ ）| A． | $2\sqrt{5}$ | B． | $4\sqrt{2}$ | C． | 6 | D． | $4\sqrt{3}$ |
分析 由三视图可得，该几何体为三棱锥，直观图为侧棱垂直于底面，侧棱长为4，底面为底边长，为4，高为4的等腰三角形，即可求出该多面体的最长的棱长．
解答 解：由三视图可得，该几何体为三棱锥，直观图为侧棱垂直于底面，侧棱长为4，底面为底边长，为4，高为4的等腰三角形，
∴多面体的最长的棱长为$\sqrt{16+4+16}$=6．
故选C．
点评 三视图中长对正，高对齐，宽相等；由三视图想象出直观图，一般需从俯视图构建直观图，本题考查了学生的空间想象力，识图能力及计算能力．
练习册系列答案
相关题目
11．把函数y=sinx（x∈R）的图象上所有点的横坐标缩短到原来的$\frac{1}{2}$倍（纵坐标不变），再把所得图象上所有向左平行移动$\frac{π}{3}$个单位长度，得到的图象所表示的函数是（ ）
| A． | $y=sin（2x-\frac{π}{3}），x∈R$ | B． | $y=sin（\frac{x}{2}+\frac{π}{6}），x∈R$ | C． | $y=sin（2x+\frac{π}{3}），x∈R$ | D． | $y=sin（2x+\frac{2π}{3}），x∈R$ |
16．如图是求样本x1，x2，…，x10平均数$\overline x$的程序框图，图中空白框中应填入的内容为（ ）
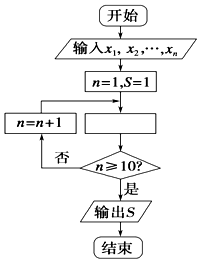
| A． | $S=S+\frac{x_n}{10}$ | B． | $S=S+\frac{x_n}{n}$ | C． | S=S+n | D． | S=S+xn |
6．若复数z满足（3-4i）z=|4+3i|，则z的虚部为（ ）
| A． | $\frac{4}{5}$ | B． | $-\frac{4}{5}$ | C． | 4 | D． | -4 |
13．已知f（x）=|2x-1|，当a＜b＜c时，有f（a）＞f（c）＞f（b），则必有（ ）
| A． | a＜0，b＜0，c＜0 | B． | a＜0，b＞0，c＞0 | C． | 2-a＜2c | D． | 1＜2a+2c＜2 |