题目内容
10.已知函数f(x)=ax3+|x-a|,a∈R.(Ⅰ)若a=-1,求函数y=f(x)在[0,+∞)的单调区间;
(Ⅱ)方程f(x)=x4有3个不同的实根,求实数a的取值范围;
(Ⅲ)当a>0时,若对于任意的x1∈[a,a+1],都存在x2∈[a+1,+∞],使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
分析 (Ⅰ)先求导,根据导数和函数单调性的关系即可求出单调区间;
(Ⅱ)若f(x)=x4,此方程等价于x=a或$\left\{\begin{array}{l}{x>a}\\{x=1}\end{array}\right.$或$\left\{\begin{array}{l}{x<a}\\{x=-1}\end{array}\right.$,分类讨论,即可讨论方程f(x)=x4的实数解的个数,即可得到答案
(Ⅲ)确定函数f(x)在(a,+∞)上是增函数,且f(x)>f(a)=a4>0,对任意的x1∈[a,a+2],都存在x2∈[a+2,+∞),使得f(x1)f(x2)=1024,所以[$\frac{1024}{f(a+1)}$,$\frac{1024}{f(a)}$]⊆[f(a+1),+∞),即可得出结论.
解答 解:(Ⅰ)当a=-1,x∈[0,+∞)时,f(x)=-x3+x+1,从而f′(x)=-3x2+1=-3(x+$\frac{\sqrt{3}}{3}$)(x-$\frac{\sqrt{3}}{3}$),
令f′(x)=0,解得x=$\frac{\sqrt{3}}{3}$,
当f′(x)<0时,即x>$\frac{\sqrt{3}}{3}$,函数单调递减,
当f′(x)>0时,即0<x<$\frac{\sqrt{3}}{3}$,函数单调递增,
所以f(x)在(0,$\frac{\sqrt{3}}{3}$)上为单调递增,在($\frac{\sqrt{3}}{3}$,+∞)上单调递减;
(Ⅱ)由f(x)=x4,即ax3+|x-a|=x4,
所以x4-ax3=|x-a|,从而x3(x-a)=|x-a|,
此方程等价于x=a或$\left\{\begin{array}{l}{x>a}\\{x=1}\end{array}\right.$或$\left\{\begin{array}{l}{x<a}\\{x=-1}\end{array}\right.$
所以当a≥1时,方程有两个不同的解a,-1,
当-1<a<1时,方程有三个不同的解a,-1,1,
当a≤-1时,方程有两个不同的解a,1,
综上,当-1<a<1时,方程有三个不同的解a,-1,1;
(Ⅲ)当a>0,x∈(a,+∞)时,f(x)=ax3+x-a,f′(x)=3ax2+1>0,
所以函数f(x)在(a,+∞)上是增函数,且f(x)>f(a)=a4>0.
所以当x∈[a,a+1],f(x)∈[a4,f(a+1)],
当x∈[a+1,+∞)时,f(x)∈[f(a+1),+∞),
所以$\frac{1024}{f(x)}$∈(0,$\frac{1024}{f(a+1)}$]
因为对任意的x1∈[a,a+1],都存在x2∈[a+1,+∞),使得f(x1)f(x2)=1024,
从而$\frac{1024}{f(a+1)}$≥f(a+1),
所以f 2(a+1)≤1024,即f(a+1)≤32,也即a(a+1)3+1≤32,
因为g(a)=a(a+1)3+1为(0,+∞)单调递增,
且g(1)=9≤32满足,而g(2)=55≥32,不满足题意,
所以a≥2时,均不满足题意,
所以满足条件的正整数a的取值的集合为{1}.
点评 本题考查利用导数研究函数的单调性,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于难题.

 寒假学与练系列答案
寒假学与练系列答案| A. | $\overrightarrow a-\overrightarrow b$ | B. | $\overrightarrow b-\overrightarrow a$ | C. | $\overrightarrow b+\overrightarrow a$ | D. | $-\overrightarrow a-\overrightarrow b$ |
 在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )
在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )| A. | $2\sqrt{5}$ | B. | $4\sqrt{2}$ | C. | 6 | D. | $4\sqrt{3}$ |
| A. | $\frac{9}{4}$ | B. | $\frac{11}{4}$ | C. | -$\frac{9}{4}$ | D. | -$\frac{11}{4}$ |
| A. | 100 | B. | 99 | C. | 98 | D. | 97 |
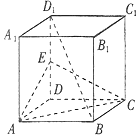 如图,正方体 A BCD-A1 B1C1D1中,E为DD1的中点.
如图,正方体 A BCD-A1 B1C1D1中,E为DD1的中点.