题目内容
6.用数学归纳法证明:n3+5n能被6整除的过程中,当n=k+1时,式子(k+1)3+5(k+1)应变形为(k3+5k)+3k(k+1)+6.分析 用数学归纳法证明:n3+5n能被6整除的过程中,当n=k+1时,式子(k+1)3+5(k+1)应变形为:(k3+5k)+3k(k+1)+6,
解答 解:用数学归纳法证明:n3+5n能被6整除的过程中,当n=k+1时,式子(k+1)3+5(k+1)应变形为:(k3+5k)+3k(k+1)+6,
由于假设k3+5k能够被6整除,而k(k+1)能够被2整除,因此3k(k+1)+6能够被6整除.
故答案为:(k3+5k)+3k(k+1)+6.
点评 本题考查了数学归纳法、乘法公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
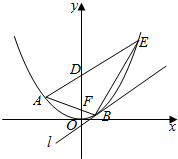 如图AB是抛物线C:x2=4y过焦点F的弦(点A在第二象限),过点A的直线交抛物线于点E,交y轴于点D(D在F上方),且|AF|=|DF|,过点B作抛物线C的切线l
如图AB是抛物线C:x2=4y过焦点F的弦(点A在第二象限),过点A的直线交抛物线于点E,交y轴于点D(D在F上方),且|AF|=|DF|,过点B作抛物线C的切线l