题目内容
2．已知扇形的圆心角为60°，其弧长为2π，则此扇形的面积为6π．分析 设扇形的半径为r，根据弧长公式可求出r的值，再由扇形的面积公式即可得出结论．
解答 解：设扇形的半径为r，
∵扇形的圆心角为60°，它的弧长为2πcm，
∴$\frac{60πr}{180}$=2π，解得r=6（cm），
∴S扇形=$\frac{1}{2}$×2π×6=6π．
故答案为：6π．
点评 本题考查的是扇形面积的计算，熟记扇形的面积公式是解答此题的关键，属于基础题．
练习册系列答案
相关题目
12．直线l1：4x+3y-1=0与直线l2：8x+6y+3=0的距离为（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
已知函数f（x）=x|x-2|．
10．在复平面内，若z=m-3+mi 所对应的点在第二象限，则实数m的取值范围是（ ）
| A． | （0，3） | B． | （-∞，-2） | C． | （-2，0） | D． | （3，4） |
17．方程x2+y2-2x+4y+6=0表示的图形为（ ）
| A． | 一个点 | B． | 一个圆 | C． | 一条直线 | D． | 不存在 |
7．执行如图的程序框图，则输出的S=（ ）
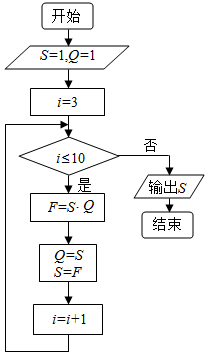
| A． | 21 | B． | 34 | C． | 55 | D． | 89 |
14．执行如图所示的程序框图，若输出的i的值为12，则①、②处可填入的条件分别为（ ）
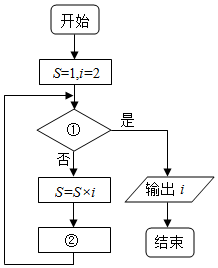
| A． | S＞384，i=i+1 | B． | S≥384，i=i+2 | C． | S＞3840，i=i+1 | D． | S≥3840，i=i+2 |
执行如图的程序框图，那么输出的a是2．