题目内容
若直线l过点P（1，1）与双曲线x2-
=1只有一个公共点，则这样的直线有（ ）
| y2 |
| 4 |
| A、4条 | B、3条 | C、2条 | D、1条 |
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：双曲线x2-
=1的渐近线方程为：y=±2x，结合双曲线的性质与图形可得过点（1，1）与双曲线公有一个公共点的直线的条数．
| y2 |
| 4 |
解答：
解：由题意可得：双曲线x2-
=1的渐近线方程为：y=±2x，
①直线x=1与双曲线只有一个公共点；
②过点P （1，1）平行于渐近线y=±2x时，直线L与双曲线只有一个公共点，方程为y-1=±2（x-1），即2x-y-1=0或2x+y-3=0
故直线l过点P（1，1）与双曲线x2-
=1只有一个公共点，则这样的直线有3条．
故选：B．
| y2 |
| 4 |
①直线x=1与双曲线只有一个公共点；
②过点P （1，1）平行于渐近线y=±2x时，直线L与双曲线只有一个公共点，方程为y-1=±2（x-1），即2x-y-1=0或2x+y-3=0
故直线l过点P（1，1）与双曲线x2-
| y2 |
| 4 |
故选：B．
点评：本题以双曲线为载体，主要考查了直线与圆锥曲线的综合问题．突出考查了双曲线的几何性质．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
cos960°=（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
在矩形ABCD中，|
|=
，|
|=1，则|
-
|=（ ）
| AB |
| 3 |
| BC |
| BA |
| BC |
| A、2 | ||
| B、3 | ||
C、2
| ||
| D、4 |
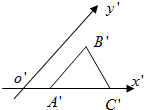如图是水平放置的△ABC的直观图，A′B′∥y′轴，A′B′=A′C′，则△ABC是（ ）| A、等边三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
已知a＞b＞0，椭圆C1的方程为
+
=1，双曲线C2的方程为
-
=1，C1与C2的离心率之积为
，则C2的渐近线方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 4 |
| A、x±2y=0 |
| B、2x±y=0 |
| C、x±4y=0 |
| D、4x±y=0 |