题目内容
已知正方体ABCD-A1B1C1D1的棱长为1,在正方体内随机取点M,求使四棱锥M-ABCD的体积小于
的概率.
| 1 |
| 6 |
考点:几何概型
专题:概率与统计
分析:算出当四棱锥M-ABCD的体积等于
时,点M到平面ABCD的距离等于
,可得当M到平面ABCD的距离小于
时,四棱锥M-ABCD的体积小于
.
由此利用长方体、正方体的体积公式和几何概型公式加以计算,可得所求概率
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
由此利用长方体、正方体的体积公式和几何概型公式加以计算,可得所求概率
解答:
解:∵正方体ABCD-A1B1C1D1的棱长为1,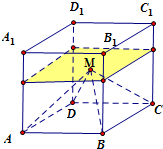
∴正方体的体积V=1×1×1=1.
当四棱锥M-ABCD的体积小于
时,设它的高为h,
则
×12h<
,解之得h<
则点M在到平面ABCD的距离等于
的截面以下时,四棱锥M-ABCD的体积小于
,
求得使得四棱锥M-ABCD的体积小于
的长方体的体积V'=1×1×
=
∴四棱锥M-ABCD的体积小于
的概率P=
=
.
故答案为:
.

∴正方体的体积V=1×1×1=1.
当四棱锥M-ABCD的体积小于
| 1 |
| 6 |
则
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
则点M在到平面ABCD的距离等于
| 1 |
| 2 |
| 1 |
| 6 |
求得使得四棱锥M-ABCD的体积小于
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
∴四棱锥M-ABCD的体积小于
| 1 |
| 6 |
| V′ |
| V |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题给出正方体的棱长,求四棱锥的体积小于
的概率.着重考查了空间几何体的体积计算和几何概型计算公式等知识,属于中档题.
| 1 |
| 6 |

练习册系列答案
相关题目
若直线l过点P(1,1)与双曲线x2-
=1只有一个公共点,则这样的直线有( )
| y2 |
| 4 |
| A、4条 | B、3条 | C、2条 | D、1条 |
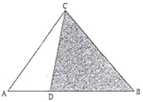 如图,在△ABC中,D是AB边上的点,且AD=
如图,在△ABC中,D是AB边上的点,且AD=| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
数列{an}中,a1=
,且(n+2)an+1=nan,则它的前20项之和S20=( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|