题目内容
14．若正实数x，y满足log2（x+3y）=log4x2+log2（2y），则3x+y的最小值是（ ）| A． | 12 | B． | 6 | C． | 16 | D． | 8 |
分析 正实数x，y满足log2（x+3y）=log4x2+log2（2y），得：x+3y=2xy，即$\frac{1}{y}+\frac{3}{x}$=2，利用“1”的代换，即可求出3x+y的最小值．
解答 解：∵正实数x，y满足log2（x+3y）=log4x2+log2（2y），
∴（x+3y）2=x2（2y）2，整理，得：x+3y=2xy，
∴$\frac{1}{y}+\frac{3}{x}$=2，
∴3x+y=$\frac{1}{2}$（3x+y）（$\frac{1}{y}+\frac{3}{x}$）=$\frac{1}{2}$（10+$\frac{3x}{y}$+$\frac{3y}{x}$）≥$\frac{1}{2}$（10+6）=8，
故选D．
点评 本题考查对数的运算，考查基本不等式的运用，属于中档题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
4．
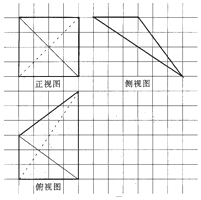如图，网格纸上小正方形的边长为1，下图画出的是某空间几何体的三视图，则该几何体的最短棱长为（ ）
如图，网格纸上小正方形的边长为1，下图画出的是某空间几何体的三视图，则该几何体的最短棱长为（ ）| A． | 4 | B． | 5 | C． | 4$\sqrt{2}$ | D． | $\sqrt{41}$ |
5．下列函数中，在（-∞，0）内为减函数的是（ ）
| A． | y=3x | B． | y=x3 | C． | y=2x+1 | D． | y=x2+1 |
2．2016年8月江西某高校的成立了一个社会实践调查小组，在对大学生的“4G使用流量问题”的调查中，随机发放了120份问卷，对收回的100份有效问卷进行统计，得到如下2×2列联表：
（1）现已按4G使用流量问题采用分层抽样从45份男生问卷中抽取了9份问卷，试问应该从“流量超过1000M”和“流量没有超过1000M”各抽取多少人？
（2）如果认为良好“4G使用流量问题”与性别有关犯错误的概率不超过P，那么根据临界值表最精确的P的值应为多少？请说明理由．
附：独立性检验统计量K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d，
独立性检验临界表：
| 流量超过1000M | 流量没有超过1000M | 合计 | |
| 男 | 20 | 25 | 45 |
| 女 | 40 | 15 | 55 |
| 合计 | 60 | 40 | 100 |
（2）如果认为良好“4G使用流量问题”与性别有关犯错误的概率不超过P，那么根据临界值表最精确的P的值应为多少？请说明理由．
附：独立性检验统计量K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d，
独立性检验临界表：
| P（K2≥k0） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
3．设i是虚数单位，若复数$a-\frac{10}{3-i}（a∈R）$是纯虚数，则a的值为（ ）
| A． | 3 | B． | -1 | C． | -3 | D． | 1 |