题目内容
5.已知A(0,2,3),B(-2,1,6),C(1,-1,5),若|$\overrightarrow{a}$|=$\sqrt{3}$,且$\overrightarrow{a}$⊥$\overrightarrow{AB}$,$\overrightarrow{a}$⊥$\overrightarrow{AC}$,则向量$\overrightarrow{a}$的坐标为(1,1,1)或(-1,-1,-1).分析 设$\overrightarrow{a}$=(x,y,z),由|$\overrightarrow{a}$|=$\sqrt{3}$,且$\overrightarrow{a}$⊥$\overrightarrow{AB}$,$\overrightarrow{a}$⊥$\overrightarrow{AC}$,列出方程组,能求出向量$\overrightarrow{a}$的坐标.
解答 解:设$\overrightarrow{a}$=(x,y,z),
∵A(0,2,3),B(-2,1,6),C(1,-1,5),
∴$\overrightarrow{AB}$=(-2,-1,3),$\overrightarrow{AC}$=(1,-3,2),
∵|$\overrightarrow{a}$|=$\sqrt{3}$,且$\overrightarrow{a}$⊥$\overrightarrow{AB}$,$\overrightarrow{a}$⊥$\overrightarrow{AC}$,
∴$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}+{z}^{2}=3}\\{-2x-y+3z=0}\\{x-3y+2z=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=1}\\{z=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-1}\\{z=-1}\end{array}\right.$.
∴向量$\overrightarrow{a}$的坐标为:(1,1,1)或(-1,-1,-1).
故答案为:(1,1,1)或(-1,-1,-1).
点评 本题考查点的坐标的求法,是基础题,解题时要认真审题,注意向量垂直的性质的合理运用.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案| A. | 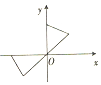 | B. | 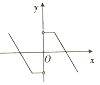 | C. |  | D. |  |
| A. | (-∞,0) | B. | (2,+∞) | C. | (0,2) | D. | (-2,2) |
| A. | $\frac{{-1+\sqrt{3}}}{2}$ | B. | $\frac{{-1+\sqrt{5}}}{2}$ | C. | $\frac{{1+\sqrt{5}}}{2}$ | D. | $2+\sqrt{5}$ |