题目内容
3．假设你家订了一份牛奶，送奶人在早上6：30～7：30之间随机地把牛奶送到你家，而你在早上7：00～8：00之间随机离家上学，则你在离家前能收到牛奶的概率是（ ）| A． | $\frac{1}{8}$ | B． | $\frac{5}{8}$ | C． | $\frac{1}{2}$ | D． | $\frac{7}{8}$ |
分析 设送牛奶人到达的时间为x，此人离家的时间为y，以横坐标表示牛奶送到时间，以纵坐标表示此人离家时间，建立平面直角坐标系，作图求面积之比即可．
解答 
解：设送奶人到达的时间为x，此人离家的时间为y，以横坐标表示奶送到时间，以纵坐标表示此人离家时间，建立平面直角坐标系（如图）则此人离开家前能收到牛奶的事件构成区域如图示，所以所求概率P=1-$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$=$\frac{7}{8}$，
故选D．
点评 本题考查几何概型的会面问题，准确作图利用面积作为几何测度是解决问题的关键，属中档题．
练习册系列答案
相关题目
13．若（x3+$\frac{1}{\sqrt{x}}$）n的展开式中含有常数项，且n的最小值为a，则${∫}_{-a}^{a}$$\sqrt{{a}^{2}-{x}^{2}}$dx=（ ）
| A． | 0 | B． | $\frac{686}{3}$ | C． | $\frac{49π}{2}$ | D． | 49π |
11．已知函数$f（x）=sin（{ωx-\frac{π}{6}}）+\frac{1}{2}（{ω＞0}）$，且$f（α）=-\frac{1}{2}$，$f（β）=\frac{1}{2}$，若|α-β|的最小值为$\frac{3π}{4}$，则ω的值为（ ）
| A． | 1 | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | 2 |
18．已知等差数列{an}的公差d＞0，且a2，a5-1，a10成等比数列，若a1=5，Sn为数列{an}的前n项和，则$\frac{{2{S_n}+n+32}}{{{a_n}+1}}$的最小值为（ ）
| A． | $3\sqrt{3}$ | B． | $2\sqrt{7}$ | C． | $\frac{20}{3}$ | D． | $\frac{17}{3}$ |
8．已知A（3，-1），B=（x，y），C（0，1）三点共线，若x，y均为正数，则$\frac{3}{x}$+$\frac{2}{y}$的最小值是（ ）
| A． | $\frac{5}{3}$ | B． | $\frac{8}{3}$ | C． | 8 | D． | 24 |
如图，已知三棱锥A-BPC中，AP⊥PC，AC⊥BC，M为AB的中点，D为PB的中点，且△PMB为正三角形．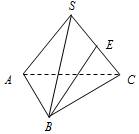
如图，三棱锥S-ABC中，若$AC=2\sqrt{3}$，SA=SB=SC=AB=BC=4，E为棱SC的中点，则直线AC与BE所成角的余弦值为$\frac{1}{4}$，直线AC与平面SAB所成的角为600．