题目内容
对任意x∈R,函数f(x)表示-x+3,
x+
,x2-4x+3中的较大者,则f(x)的最小值是 .
| 3 |
| 2 |
| 1 |
| 2 |
考点:函数的最值及其几何意义,函数的图象
专题:计算题,作图题,函数的性质及应用
分析:由题意比较三者之间的大小,从而可得f(x)=
,从而求最小值.
|
解答:
 解:由
解:由
x+
-(-x+3)>0得,x>1;
由x2-4x+3-(-x+3)>0得,x>3或x<0;
由x2-4x+3-(
x+
)>0得,x>5或x<
;
则f(x)=
;
结合函数的图象如下,
fmin(x)=f(1)=-1+3=2;
故答案为:2.
 解:由
解:由| 3 |
| 2 |
| 1 |
| 2 |
由x2-4x+3-(-x+3)>0得,x>3或x<0;
由x2-4x+3-(
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则f(x)=
|
结合函数的图象如下,
fmin(x)=f(1)=-1+3=2;
故答案为:2.
点评:本题考查了分段函数的化简与应用,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
实数x,y满足
,则z=3x-y的最小值是( )
|
| A、-4 | B、-2 | C、0 | D、4 |
执行如图中的程序框图,若p=0.8,则输出的n=( )
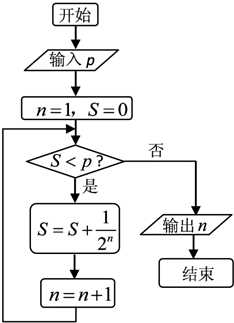

| A、2 | B、3 | C、5 | D、4 |



