题目内容

设正整数数列{an}满足:a2=4,且对于任何n∈N*,有2+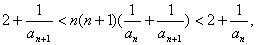

(1)求a1、a3;

(2)求数列{an}的通项an.

解：(1)据条件得              ①

当n=1时,由

解得.因为a1为正整数,故a1=1.

当n=2时,由

解得8＜a3＜10,所以a3=9.

(2)由a1=1,a2=4,a3=9,猜想:an=n2,

下面用数学归纳法证明:

①当n=1,2时,由(1)知an=n2均成立;

②假设n=k(k≥2)成立,

即ak=k2,则n=k+1时,

由①得

因为k≥2时,(k3+1)-(k+1)2=k(k+1)(k-2)≥0,

所以∈(0,1］.

k-1≥1,所以∈(0,1］.

又ak+1∈N*,所以(k+1)2≤ak+1≤(k+1)2.

故ak+1=(k+1)2,即n=k+1时,an=n2成立.

由①②,知对任意n∈N*,an=n2.

练习册系列答案
相关题目
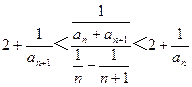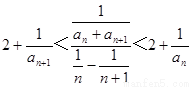设正整数数列{an}满足：a2=4，且对于任何n∈N*，有2+
1
an+1
＜
1
an
+
1
an+1
1
n
-
1
n+1
＜2+
1
an
；
（1）求a1，a3；
（2）求数列{an}的通项an．
设正整数数列{an}满足a1=2，a2=6，当n≥2时，有|
a
2
n
-an-1an+1| ＜  
1
2
an-1．
（1）求a3的值；（2）求数列{an}的通项；
（3）记Tn=
12
a1
+
22
a2
+
32
a3
 +K+
n2
an
，证明：对任意n∈N*，Tn＜
9
4
．
设正整数数列{an}满足：a2=4，且对于任何n∈N*，有2+
1
an+1
＜
1
an
+
1
an+1
1
n
-
1
n+1
＜2+
1
an
，则a10=
100
100
．

（本小题满分14分）
设正整数数列{an}满足：a2＝4，且对于任何
n∈N*，有．
（1）求a1，a3；
（2）求数列{ an }的通项an．

（本小题满分14分）

设正整数数列{an}满足：a2＝4，且对于任何

n∈N*，有．

   （1）求a1，a3；

   （2）求数列{ an }的通项an ．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网