题目内容
已知函数 .
.(1)若m=-3,求函数g(x)的单调区间;
(2)若对于任意t∈[1,2],函数g(x)在区间(t,3)上总不为单调函数,求实数m的取值范围.
【答案】分析:(1)当m=-3时,g'(x)=3x2+x-2=(x+1)(3x-2),由此能求出函数g(x)的单调区间.
(2)g'(x)=3x2+(m+4)x-2,由g′(0)=-2,对于任意t∈[1,2],函数g(x)在区间(t,3)上总不为单调函数,知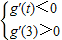 ,由此能求出实数m的取值范围.
,由此能求出实数m的取值范围.
解答:解:(1)当m=-3时,g'(x)=3x2+x-2=(x+1)(3x-2),
由g'(x)=(x+1)(3x-2)>0,得x<-1,或x> ;
;
由g'(x)=(x+1)(3x-2)<0,得-1<x< ,
,
∴增区间: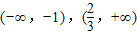 ,减区间:(-1,
,减区间:(-1, )
)
(2)g'(x)=3x2+(m+4)x-2,
∵g′(0)=-2,对于任意t∈[1,2],函数g(x)在区间(t,3)上总不为单调函数,
∴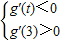 ,
,
∴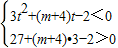 ,
,
∴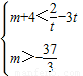 ,
,
解得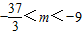 ,
,
∴实数m的取值范围是{m|-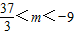 }.
}.
点评:本题考查利用导数研究函数的单调性,考查等价转化能力和运算能力,解题时要认真审题,仔细解答,注意不等式知识的合理运用.
(2)g'(x)=3x2+(m+4)x-2,由g′(0)=-2,对于任意t∈[1,2],函数g(x)在区间(t,3)上总不为单调函数,知
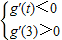 ,由此能求出实数m的取值范围.
,由此能求出实数m的取值范围.解答:解:(1)当m=-3时,g'(x)=3x2+x-2=(x+1)(3x-2),
由g'(x)=(x+1)(3x-2)>0,得x<-1,或x>
 ;
;由g'(x)=(x+1)(3x-2)<0,得-1<x<
 ,
,∴增区间:
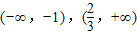 ,减区间:(-1,
,减区间:(-1, )
)(2)g'(x)=3x2+(m+4)x-2,
∵g′(0)=-2,对于任意t∈[1,2],函数g(x)在区间(t,3)上总不为单调函数,
∴
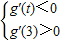 ,
,∴
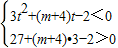 ,
,∴
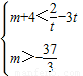 ,
,解得
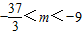 ,
,∴实数m的取值范围是{m|-
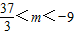 }.
}.点评:本题考查利用导数研究函数的单调性,考查等价转化能力和运算能力,解题时要认真审题,仔细解答,注意不等式知识的合理运用.

练习册系列答案
相关题目
 ,
, ,判断f(x)在(1,+∞)上的单调性,并给予证明.
,判断f(x)在(1,+∞)上的单调性,并给予证明.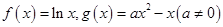 .
. 与
与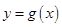 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数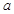 的值及点P的坐标;
的值及点P的坐标; .
.