题目内容
已知函数![]() .
.
(1)若f(x)图象左移θ单位后对应函数为偶函数,求θ的值;
(2)若![]() 时,不等式f(x)>m恒成立,求实数m的取值范围.
时,不等式f(x)>m恒成立,求实数m的取值范围.
考点:
二倍角的余弦;诱导公式的作用;两角和与差的正弦函数;正弦函数的单调性.
专题:
三角函数的图像与性质.
分析:
(1)利用三角函数的恒等变换化简函数f(x)的解析式,再根据左移θ后对应函数为偶函数,求得θ的值.
(2)根据![]() 时,不等式f(x)>m恒成,可得m<f(x)min,再由
时,不等式f(x)>m恒成,可得m<f(x)min,再由![]() ,求得f(x)的最小值,从而求得m的取值范围.
,求得f(x)的最小值,从而求得m的取值范围.
解答:
解:(1)![]()
![]() …(4分)
…(4分)
∵左移θ后对应函数为偶函数,∴![]() ,
,![]()
∴![]() …(7分)
…(7分)
(2)∵![]() 时,不等式f(x)>m恒成立,∴m<f(x)min ,(9分)
时,不等式f(x)>m恒成立,∴m<f(x)min ,(9分)
而![]() ,∴f(x)min=2,
,∴f(x)min=2,
∴m的取值范围是(﹣∞,2).…(14分)
点评:
本题主要考查三角函数的恒等变换,正弦函数的单调性、定义域和值域,函数的恒成立问题,属于中档题.

练习册系列答案
相关题目
 ,
,
 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: .
.
 .
. 为
为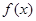 的极值点,求实数
的极值点,求实数 的值;
的值; 在
在 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. 。
。 ,求函数
,求函数 的值;
的值; .
.
 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素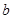 ,求方程
,求方程 有两个不相等实根的概率;
有两个不相等实根的概率; 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程