题目内容
已知函数 ,
,
(1)若m∈Z,判定f(x)的奇偶性;
(2)若 ,判断f(x)在(1,+∞)上的单调性,并给予证明.
,判断f(x)在(1,+∞)上的单调性,并给予证明.
解:(1)m是奇数时,定义域是{ x|x≠0},
f(-x)=-f(x),f(x)为奇函数,
m为偶数时,定义域是{ x|x≠0},
f(-x)≠-f(x)且f(-x)≠f(x),
f(x)既不是奇函数也不是偶函数;
(2)由 ,得m=2,∴
,得m=2,∴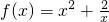 ,
,
f(x)在(1,+∞)上的单调增函数,
证明:设a>b>1,f(a)-f(b)=a2+ -b2-
-b2- =(a+b)(a-b)-
=(a+b)(a-b)-
=(a-b)(a+b- )
)
∵a>b>1,∴a-b>0,a+b> ,∴(a-b)(a+b-
,∴(a-b)(a+b- )>0,
)>0,
∴f(a)-f(b)>0,f(x)在(1,+∞)上的单调增函数.
分析:(1)分m是奇数,m为偶数两种情况来讨论,考查定义域及f(-x)与f(x)的关系,依据奇偶性的定义进行判断.
(2)由 ,得m=2,从而得到f(x)的解析式,设a>b>1,化简f(a)-f(b)的表达式为因式乘积的形式,判断符号,得出结论.
,得m=2,从而得到f(x)的解析式,设a>b>1,化简f(a)-f(b)的表达式为因式乘积的形式,判断符号,得出结论.
点评:本题考查判断函数奇偶性的方法及步骤,体现分类讨论的数学思想.
f(-x)=-f(x),f(x)为奇函数,
m为偶数时,定义域是{ x|x≠0},
f(-x)≠-f(x)且f(-x)≠f(x),
f(x)既不是奇函数也不是偶函数;
(2)由
 ,得m=2,∴
,得m=2,∴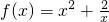 ,
,f(x)在(1,+∞)上的单调增函数,
证明:设a>b>1,f(a)-f(b)=a2+
 -b2-
-b2- =(a+b)(a-b)-
=(a+b)(a-b)-
=(a-b)(a+b-
 )
)∵a>b>1,∴a-b>0,a+b>
 ,∴(a-b)(a+b-
,∴(a-b)(a+b- )>0,
)>0,∴f(a)-f(b)>0,f(x)在(1,+∞)上的单调增函数.
分析:(1)分m是奇数,m为偶数两种情况来讨论,考查定义域及f(-x)与f(x)的关系,依据奇偶性的定义进行判断.
(2)由
 ,得m=2,从而得到f(x)的解析式,设a>b>1,化简f(a)-f(b)的表达式为因式乘积的形式,判断符号,得出结论.
,得m=2,从而得到f(x)的解析式,设a>b>1,化简f(a)-f(b)的表达式为因式乘积的形式,判断符号,得出结论.点评:本题考查判断函数奇偶性的方法及步骤,体现分类讨论的数学思想.

练习册系列答案
相关题目
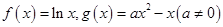 .
. 与
与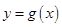 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数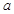 的值及点P的坐标;
的值及点P的坐标; .
. .
.