题目内容
1．设函数$f（x）=\left\{\begin{array}{l}{3^{-x}}-2\\ \sqrt{x}\end{array}\right.\begin{array}{l}x≤0\\ x＞0\end{array}$，若f（x0）=1，则x0=±1．分析 根据函数解析式对x0分类讨论，分别代入方程化简求出x0的值．
解答 解：由题意知，$f（x）=\left\{\begin{array}{l}{3^{-x}}-2\\ \sqrt{x}\end{array}\right.\begin{array}{l}x≤0\\ x＞0\end{array}$，
①当x0＞0时，方程f（x0）=1是$\sqrt{{x}_{0}}=1$
解得x0=1；
②当x0≤0时，方程f（x0）=1是${3}^{-{x}_{0}}-2=1$，
则${3}^{-{x}_{0}}=3$，解得x0=-1，
综上，x0=±1，
故答案为：±1．
点评 本题考查分段函数与方程根的问题，以及分类讨论思想，属于基础题．
练习册系列答案
相关题目
9．一个几何体的三视图如图所示，则该几何体的体积为（ ）
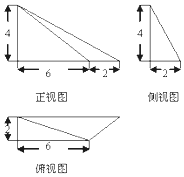
| A． | $\frac{56}{3}$ | B． | $\frac{112}{3}$ | C． | $\frac{119}{3}$ | D． | $\frac{128}{3}$ |
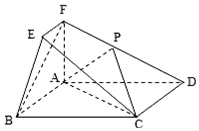在如图所示的几何体中，四边形ABCD为矩形，平面ABCD⊥平面ABEF，EF∥AB，∠BAF=90°，AD=2，AB=AF=2EF=1，点P在棱DF上．