题目内容
11.已知x,y∈[0,2π],若$2sinxcosy-sinx+cosy=\frac{1}{2}$,则x-y的最小值为-$\frac{π}{2}$.分析 由已知整理可得(sinx+$\frac{1}{2}$)(cosy-$\frac{1}{2}$)=0,解得sinx=-$\frac{1}{2}$或cosy=$\frac{1}{2}$,结合范围x,y∈[0,2π],即可求解x-y的最小值.
解答 解:∵2sinxcosy-sinx+cosy=$\frac{1}{2}$,
∴2sinxcosy-sinx+cosy-$\frac{1}{2}$=0,
∴sinxcosy-$\frac{1}{2}$sinx+$\frac{1}{2}$cosy-$\frac{1}{4}$=0,
∴(sinx+$\frac{1}{2}$)(cosy-$\frac{1}{2}$)=0,
∴sinx=-$\frac{1}{2}$或cosy=$\frac{1}{2}$,
∵x,y∈[0,2π]
∴x=$\frac{7π}{6}$或$\frac{11π}{6}$,y=$\frac{π}{3}$或$\frac{5π}{3}$,
当x=$\frac{7π}{6}$,y=$\frac{5π}{3}$时,x-y取得最小值,最小值为$\frac{7π}{6}$-$\frac{5π}{3}$=-$\frac{π}{2}$.
故答案为:-$\frac{π}{2}$.
点评 本题主要考查了特殊角的三角函数值,三角函数的图象和性质的应用,考查了转化思想,属于基础题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
19.下列四个函数中,与y=x表示同一函数的是( )
| A. | y=$\sqrt{x}$ | B. | $y=\frac{x^2}{x}$ | C. | $y=\sqrt{x^2}$ | D. | $y=\root{3}{x^3}$ |
6.下列表示正确的是( )
| A. | {1}∈{1,3} | B. | 1⊆{1,2} | C. | ∅∈{0} | D. | ∅⊆∅ |
16.已知全集U=R,集合A={x|-1<x<2},集合B={x|0<x<3},则集合∁U(A∩B)=( )
| A. | {x|x≤0或x≥2} | B. | {x|x<0或x>2} | C. | {x|x<-1或x>3} | D. | {x|x≤-1或x≥3} |
3.已知集合A={ x|$\frac{1}{x-1}$≥1},集合B={ x|log2x<1},则 A∩B=( )
| A. | (-∞,2) | B. | (0,1) | C. | (0,2) | D. | (1,2) |
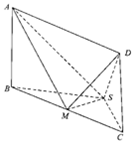 如图,在四棱锥S-ABCD中,底面ABCD是矩形,平面ABCD⊥平面SBC,SB=SC,M是BC的中点,AB=1,BC=2.
如图,在四棱锥S-ABCD中,底面ABCD是矩形,平面ABCD⊥平面SBC,SB=SC,M是BC的中点,AB=1,BC=2.