题目内容
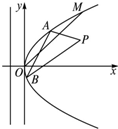 如图,在直角坐标系xOy中,点P(1,
如图,在直角坐标系xOy中,点P(1,| 1 |
| 2 |
| 5 |
| 4 |
(1)求p,t的值;
(2)用m表示△ABP 的面积S;
(3)求△ABP面积S的最大值.
分析:(1)由题意知
,由此能求出结果.
(2)设A(x1,y1),B(x2,y2),由OM过AB的中点,而且直线OM的方程为x-y=0,知线段AB的中点Q(m,m),设直线AB的斜率为k(k≠0),由
,得(y1-y2)(y1+y2)=x1-x2,故k•2m=1,直线AB的方程为y-m=
(x-m),由此能用m表示△ABP 的面积S.
(3)令u=
,0<u≤
,S=u(1-2u2),设S(u)=u(1-2u2),0<u≤
,则S′(u)=1-6u2,由此能求出△ABP面积的最大值.
|
(2)设A(x1,y1),B(x2,y2),由OM过AB的中点,而且直线OM的方程为x-y=0,知线段AB的中点Q(m,m),设直线AB的斜率为k(k≠0),由
|
| 1 |
| 2m |
(3)令u=
| m-m2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵在直角坐标系xOy中,
点P(1,
)到抛物线C:y2=2px(p>0)的准线的距离为
,
点M(t,1)是C上的定点,
∴
,
解得
.
(2)设A(x1,y1),B(x2,y2),
∵OM过AB的中点,而且直线OM的方程为x-y=0,
∴线段AB的中点Q(m,m),
由题意,设直线AB的斜率为k(k≠0),
由
,得(y1-y2)(y1+y2)=x1-x2,故k•2m=1,
∴直线AB的方程为y-m=
(x-m),
即x-2my+2m2-m=0,
由
,消去x,得y2-2my+2m2-m=0,
∴y1+y2=2m,y1y2=2m2-m,
由△=4m-4m2>0,得0<m<1,
从而|AB|=
•|y1-y2|=
•
,
设点P到直线AB的距离为d,
则d=
,
设△ABP的面积为S,
则S=
|AB|•d=|1-2(m-m2)|•
,(0<m<1).

(3)令u=
,0<u≤
,
则S=u(1-2u2),
设S(u)=u(1-2u2),0<u≤
,
则S′(u)=1-6u2,
由S′(u)=0,得u=
∈(0,
),
∴S(u)max=S(
)=
.
故△ABP面积的最大值为
.
点P(1,
| 1 |
| 2 |
| 5 |
| 4 |
点M(t,1)是C上的定点,
∴
|
解得
|
(2)设A(x1,y1),B(x2,y2),
∵OM过AB的中点,而且直线OM的方程为x-y=0,
∴线段AB的中点Q(m,m),
由题意,设直线AB的斜率为k(k≠0),
由
|
∴直线AB的方程为y-m=
| 1 |
| 2m |
即x-2my+2m2-m=0,
由
|
∴y1+y2=2m,y1y2=2m2-m,
由△=4m-4m2>0,得0<m<1,
从而|AB|=
1+
|
| 1+4m2 |
| 4m-4m2 |
设点P到直线AB的距离为d,
则d=
| |1-2m+2m2| | ||
|
设△ABP的面积为S,
则S=
| 1 |
| 2 |
| m-m2 |

(3)令u=
| m-m2 |
| 1 |
| 2 |
则S=u(1-2u2),
设S(u)=u(1-2u2),0<u≤
| 1 |
| 2 |
则S′(u)=1-6u2,
由S′(u)=0,得u=
| ||
| 6 |
| 1 |
| 2 |
∴S(u)max=S(
| ||
| 6 |
| ||
| 9 |
故△ABP面积的最大值为
| ||
| 9 |
点评:本题考查直线与圆锥曲线的综合应用,具体涉及到直线方程的求法,抛物线的简单性质,点到直线的距离公式,解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.
(2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.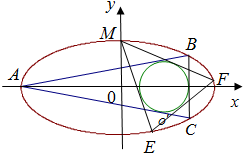 如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为 (2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
(2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且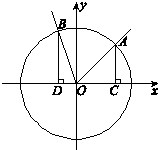 如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: