题目内容
9.观察(x2)′=2x,(x4)′=4x3,(cos x)′=-sin x,若定义在R上的函数f(x)满足f(-x)=f(x),f′(x)为f(x)的导函数,则f′(-x)=( )| A. | f(x) | B. | -f(x) | C. | f′(x) | D. | -f′(x) |
分析 由已知中(x2)'=2x,(x4)'=4x3,(cosx)'=-sinx,…分析其规律,我们可以归纳推断出,偶函数的导函数为奇函数,再结合函数奇偶性的性质,即可得到答案.
解答 解:由(x2)'=2x中,原函数为偶函数,导函数为奇函数;
(x4)'=4x3中,原函数为偶函数,导函数为奇函数;
(cosx)'=-sinx中,原函数为偶函数,导函数为奇函数;
…
我们可以推断,偶函数的导函数为奇函数.
若定义在R上的函数f(x)满足f(-x)=f(x),
则函数f(x)为偶函数,
又∵f′(x)为f(x)的导函数,则f′(x)奇函数
故f′(-x)=-f′(x)
故选:D.
点评 本题考查的知识点是归纳推理,及函数奇偶性的性质,其中根据已知中原函数与导函数奇偶性的关系,得到结论是解答本题的关键

练习册系列答案
相关题目
8.若x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≤0}\\{y≥0}\end{array}\right.$,则z=|y-2x|的最大值为( )
| A. | 8 | B. | 6 | C. | 4 | D. | 1 |
9.小明同学的QQ密码是由0,1,2,3,4,5,6,7,8,9这10个数字中的6个数字组成的六位数,由于长时间未登录QQ,小明忘记了密码的最后两个数字,如果小明登录QQ时密码的最后两个数字随意选取,则恰好能登录的概率是( )
| A. | $\frac{1}{1{0}^{5}}$ | B. | $\frac{1}{1{0}^{4}}$ | C. | $\frac{1}{1{0}^{2}}$ | D. | $\frac{1}{10}$ |
4.已知a>0,a≠1,x≠0,则${log_{a^2}}{x^2}$=( )
| A. | 2logax | B. | logax | C. | 2loga|x| | D. | loga|x| |
18.执行如图所示的程序框图,输出的S值为8,则判断条件是( )
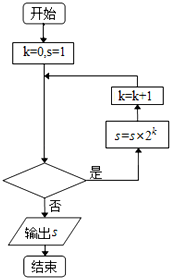

| A. | k<2 | B. | k<4 | C. | k<3 | D. | k≤3 |