题目内容
已知3a+13b=17a，5a+7b=11b，试判断a、b的大小并证明．
考点：不等式比较大小
专题：不等式
分析：利用反证法证明，先假设a≥b，再构造函数，利用函数的单调性，得出a＜1＜b，这与假设相矛盾，问题得以证明
解答：
解：假设a≥b，则13a≥13b，5a≥5b，
由3a+13b=17a得3a+13a≥17a，
即(
)a+(
)a≥1，
由f（x）=(
)x+(
)x单调递减，
∴f（1）=
+
=
＜1，且f（a）≥1＞f（1），
则a＜1，
由5a+7b=11b，得5b+7b≤11b，
即(
)b+(
)b≤1，
由g（x）=(
)x+(
)x单调递减，
∴g（1）=
+
=
＞1，且g（a）≤1＜g（1），
则b＞1，
因此a＜1＜b，这与假设相矛盾，
故假设不成立，
故a＜b．
由3a+13b=17a得3a+13a≥17a，
即(
| 3 |
| 17 |
| 13 |
| 17 |
由f（x）=(
| 3 |
| 17 |
| 13 |
| 17 |
∴f（1）=
| 3 |
| 17 |
| 13 |
| 17 |
| 16 |
| 17 |
则a＜1，
由5a+7b=11b，得5b+7b≤11b，
即(
| 5 |
| 11 |
| 7 |
| 11 |
由g（x）=(
| 5 |
| 11 |
| 7 |
| 11 |
∴g（1）=
| 5 |
| 11 |
| 7 |
| 11 |
| 12 |
| 11 |
则b＞1，
因此a＜1＜b，这与假设相矛盾，
故假设不成立，
故a＜b．
点评：本题主要考查了反证法，关键是利用反证法的步骤，找到与假设相矛盾的问题，属于难题
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
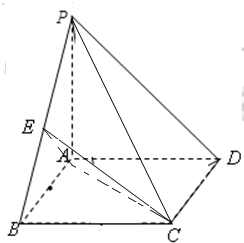如图，在四棱锥P-ABCD中，底面ABCD为矩形，侧棱PA⊥底面，且AB=2，BC=1，PA=2，E为PD的中点．