题目内容
设A、P是椭圆
+y2=1两点，点A关于x轴的对称点为B（异于点P），若直线AP、BP分别交x轴于点M、N，则
•
=（ ）
| x2 |
| 2 |
| OM |
| ON |
| A、0 | ||
| B、1 | ||
C、
| ||
| D、2 |
考点：椭圆的简单性质
专题：
分析：令椭圆的上顶点为A，下顶点为B，左端点为P，取特殊值能够简化运算．
解答：
解：如图，取特殊值，
令椭圆的上顶点为A，下顶点为B，左端点为P，
则A（0，1），B（0，-1），P（
，0），
M（
，0），N（
，0），
∴
=
=(
，0)，
∴
•
=2．
故选：D．
解：如图，取特殊值，令椭圆的上顶点为A，下顶点为B，左端点为P，
则A（0，1），B（0，-1），P（
| 2 |
M（
| 2 |
| 2 |
∴
| OM |
| ON |
| 2 |
∴
| OM |
| ON |
故选：D．
点评：本题考查椭圆中向量的数量积的求法，在选取题中恰当地选择特殊值能够大大地简化运算．
练习册系列答案
阅读快车系列答案
相关题目
执行如图所示的程序框图，输出S的值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若[x]表示不超过x的最大整数，如[2.1]=2，[-2.1]=-3．执行如图所示的程序框图，则输出的S值为（ ）如图，这是计算
+
+
+…
的值的一个程序框图，其中判断框内填入的条件是（ ）
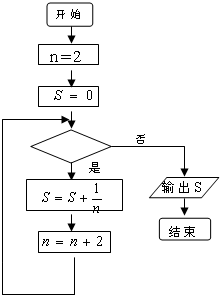
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |
| A、n＜20？ |
| B、n＜21？ |
| C、n＞19？ |
| D、n＞20？ |
已知函数f（x）=acosx+bx2-
x，若f′（x0）=0则f′（-x0）=（ ）
| 2 |
| A、0 | ||
| B、2a | ||
| C、2b | ||
D、-2
|