题目内容

已知等差数列{an}中，前n项和为Sn，若a3+a9=6，则S11=
 
．
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：利用等差数列的通项公式和前n项和公式直接求解．
解答： 解：∵等差数列{an}中，前n项和为Sn，a3+a9=6，
∴S11=
11
2
（a1+a11）=
11
2
(a3+a9)=33．
故答案为：33．
点评：本题考查等差数列的前n项和的求法，是基础题，解题时要认真审题，注意等差数列的通项公式的合理运用．
练习册系列答案
相关题目
在△ABC中，角A，B，C的对边分别为a，b，c，若（a2+c2-b2）tanB=
2
ac，则角B的值为（　　）
A、
π
4
B、
π
6
C、
π
4
或
3π
4
D、
π
6
或
5π
6
定义在R上的函数f（x）满足f（x+2）=f（x），当x∈[1，3]，f（x）=2-|x-2|，则下列结论中正确的是（　　）
A、f（sin
π
6
）＜f（cos
π
6
）
B、f（sin1）＞f（cos1）
C、f（cos
2π
3
）＜f（sin
2π
3
）
D、f（cos2）＞f（sin2）
设P（x0，y0）为椭圆
x2
4
+y=1内一定点（不在坐标轴上），过点P的两直线分别与椭圆交于A，C和B，D，若AB∥CD．
（Ⅰ）证明：直线AB的斜率为定值；
（Ⅱ）过点P作AB的平行线，与椭圆交于E，F两点，证明：点P平分线段EF．
某班学生的数学分数的茎叶图和频率分布直方图的一部分如图1、2所示，已知分数的中位数为74.5．
（Ⅰ）求茎叶图中第三组和第五组频数，并将频率分布直方图补充完整；
（Ⅱ）若把成绩最好的两位同学与第一组四位同学组成学习小组，从学习小组中随机抽两位同学担任组长，求抽到的两位同学中恰有一位在第一组的概率．
甲、乙两人玩一种猜拳游戏，游戏规则如下：每人只出一只手（有5个手指头），每次出手指数为0，1，2，3，4，5是等可能的，猜拳一次只猜“单”与“双”两个结果．规定：两人手指数之和为偶数则规定猜“双”者获胜，手指数之和为奇数视为猜“单”者获胜，两人都猜中与两人都没猜中视为平局，获胜方得2分，负方得0分，平局各得1分，只要有人累计得分达到4分或者4分以上，则游戏结束．
（1）求甲、乙两人猜拳一次，甲获胜的概率；
（2）求游戏结果时，甲累计得分恰好为4分的概率．
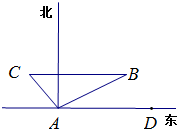如图，海警观察站设在海岸A处，某天值班海警发现北偏东60°方向，距离A处10
3
海里的B处有一艘走私船，于是给缉私船一号和缉私船二号下命令，让两艘船一起围追该走私船，接到命令后，一号缉私船在A处北偏西30°方向，距离A处10海里的C处以10
3
海里每小时的速度追截走私船，二号缉私船在A的正东方向，距离A处20海里的D处以v海里每小时速度追截走私船，走私船正以10海里每小时的速度从B处向北偏东30°方向逃窜．
（Ⅰ）两缉私船在接到命令时，相距多少海里；
（Ⅱ）若一号缉私船和二号缉私船恰好能以最短的时间同时追上走私船，求最短时间和二号缉私船的速度v．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）过点M（1，-
6
2
），F（-
2
，0）是其左焦点，P，Q是椭圆C上不同的两个动点，且|PF|，|MF|，|QF|成等差数列．
（Ⅰ）求椭圆C的方程；
（Ⅱ）证明：线段PQ的垂直平分线经过一个定点．
已知等比数列{an}的前n项和为Sn，若a52=2a3a6，S5=-62，则a1的值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网