题目内容
某班学生的数学分数的茎叶图和频率分布直方图的一部分如图1、2所示,已知分数的中位数为74.5.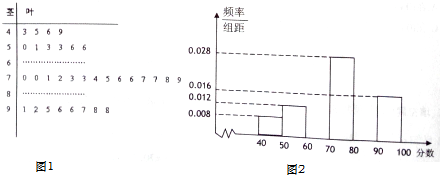
(Ⅰ)求茎叶图中第三组和第五组频数,并将频率分布直方图补充完整;
(Ⅱ)若把成绩最好的两位同学与第一组四位同学组成学习小组,从学习小组中随机抽两位同学担任组长,求抽到的两位同学中恰有一位在第一组的概率.

(Ⅰ)求茎叶图中第三组和第五组频数,并将频率分布直方图补充完整;
(Ⅱ)若把成绩最好的两位同学与第一组四位同学组成学习小组,从学习小组中随机抽两位同学担任组长,求抽到的两位同学中恰有一位在第一组的概率.
考点:古典概型及其概率计算公式,频率分布直方图,茎叶图
专题:概率与统计
分析:(1)首先根据各个小组的频率和等于1,计算第三组和第五组的频率,再根据频数=频率×总数进行计算,再将频率分布直补充完整;
(2)求抽到的两位同学中恰有一位在第一组的概率.
(2)求抽到的两位同学中恰有一位在第一组的概率.
解答:
 解:对照直方图和茎叶图可知总人数为
解:对照直方图和茎叶图可知总人数为
=50人
(1)由中位数74.5可知,74是从低到的第25名,
故第三组8人,第五组10人,
则第三组矩形高
×
=0.016,
第五组矩形高
×
=0.02
(2)设第一组四名学生编号1、2、3、4,成绩最好的两位同学编号5、6,
抽取2位同学的状况是(1,2)(1,3)(1,4)(1,5)(1,6)(2,3)
(2,4)(2,5)(2,6)(3,4)(3,5)(3,6)(4,5)(4,6)(5,6)共15种
设A表示“抽到的两位同学中成绩恰有一位在第一组”,
则A包括(1,5)(1,6)(2,5)(2,6)(3,5)(3,6)(4,5)(4,6)共8种
∴P(A)=
 解:对照直方图和茎叶图可知总人数为
解:对照直方图和茎叶图可知总人数为| 4 |
| 0.008×10 |
(1)由中位数74.5可知,74是从低到的第25名,
故第三组8人,第五组10人,
则第三组矩形高
| 8 |
| 50 |
| 1 |
| 10 |
第五组矩形高
| 10 |
| 50 |
| 1 |
| 10 |
(2)设第一组四名学生编号1、2、3、4,成绩最好的两位同学编号5、6,
抽取2位同学的状况是(1,2)(1,3)(1,4)(1,5)(1,6)(2,3)
(2,4)(2,5)(2,6)(3,4)(3,5)(3,6)(4,5)(4,6)(5,6)共15种
设A表示“抽到的两位同学中成绩恰有一位在第一组”,
则A包括(1,5)(1,6)(2,5)(2,6)(3,5)(3,6)(4,5)(4,6)共8种
∴P(A)=
| 8 |
| 15 |
点评:此题主要考查了频数、频率、频数分布直方图等知识,注意各个小组的频率和等于1,频数=频率×数据总和.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
已知α是第四象限的角,若cosα=
,则tan2α=( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
=(1,2-x),
=(2+x,3),则“|
|=
”是“向量
与
共线”的( )
| a |
| b |
| a |
| 2 |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |