题目内容
16.袋中有5只大小相同的乒乓球,编号为1至5,从袋中随机抽取3只,若以ξ表示取到球中的最大号码,则ξ的数学期望是$\frac{9}{2}$.分析 由已知得ξ的可能取值为3,4,5,分别求出相应的概率,由此能求出E(ξ).
解答 解:由已知得ξ的可能取值为3,4,5,
P(ξ=3)=$\frac{{C}_{3}^{3}}{{C}_{5}^{3}}$=$\frac{1}{10}$,
P(ξ=4)=$\frac{{C}_{3}^{2}}{{C}_{5}^{3}}$=$\frac{3}{10}$,
P(ξ=5)=$\frac{{C}_{4}^{2}}{{C}_{5}^{3}}$=$\frac{6}{10}$,
∴E(ξ)=$3×\frac{1}{10}+4×\frac{3}{10}+5×\frac{6}{10}$=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查离散型随机变量的数学期望的求法,是基础题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
11.已知三棱锥三视图如图所示,其中俯视图是边长为$\sqrt{3}$的正三角形,则该几何体的外接球的体积为( )
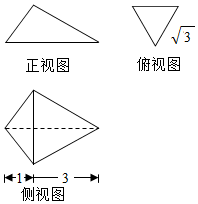

| A. | $\frac{16π}{3}$ | B. | $\frac{32π}{3}$ | C. | 4$\sqrt{3}$ | D. | 16π |
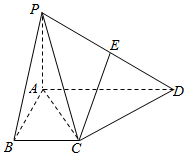 在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.
在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.