��Ŀ����
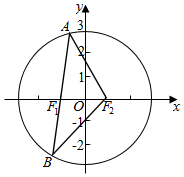
1������ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ΪF1��F2������F1��ֱ������ԲC�ཻ��A��B���㣬��$\overrightarrow{A{F}_{1}}$=$\frac{3}{2}$$\overrightarrow{{F}_{1}B}$����AF2B=90�㣬����ԲC����������$\frac{\sqrt{5}}{5}$������ ����������|BF1|=2t��|AF1|=3t������Բ�Ķ��壬�ɵ�|AF2|=2a-3t��|BF2|=2a-2t�����ù��ɶ������ɵ�t=$\frac{1}{3}$a�����cosB����F1BF2�У��������Ҷ����������ʹ�ʽ���㼴�ɵõ�����ֵ��
���  �⣺��$\overrightarrow{A{F}_{1}}$=$\frac{3}{2}$$\overrightarrow{{F}_{1}B}$������|BF1|=2t��|AF1|=3t��
�⣺��$\overrightarrow{A{F}_{1}}$=$\frac{3}{2}$$\overrightarrow{{F}_{1}B}$������|BF1|=2t��|AF1|=3t��
����Բ�Ķ��壬�ɵ�|AF2|=2a-3t��|BF2|=2a-2t��
�ɡ�AF2B=90��ɵ�|AB|2=|AF2|2+|BF2|2��
����5t��2=��2a-3t��2+��2a-2t��2��
���t=$\frac{1}{3}$a��|AB|=$\frac{5}{3}$a��|BF2|=$\frac{4}{3}$a��
�ڡ�ABF2�У�cosB=$\frac{|B{F}_{2}|}{|AB|}$=$\frac{4}{5}$��
�ڡ�F1BF2�У�cosB=$\frac{\frac{4}{9}{a}^{2}+\frac{16}{9}{a}^{2}-4{c}^{2}}{2•\frac{2}{3}a•\frac{4}{3}a}$=$\frac{4}{5}$��
����ɵ�$\frac{9}{4}$•$\frac{{c}^{2}}{{a}^{2}}$=$\frac{9}{20}$��
��e2=$\frac{1}{5}$����Ϊe=$\frac{\sqrt{5}}{5}$��
�ʴ�Ϊ��$\frac{\sqrt{5}}{5}$��
���� ���⿼����Բ�������ʵ���ע��������Բ�Ķ��壬�����εĹ��ɶ��������Ҷ����������������߶��������黯�����������������������е��⣮

| A�� | e | B�� | e2 | C�� | 2e | D�� | 2e2 |
����b?����a?������a��b���ǡ�a�Φ����ij�ֲ���Ҫ����
����a?����b?�������Φ¡��ǡ����Φ���b�Φ¡��ij�Ҫ������
�ж���ȷ���ǣ�������
| A�� | �٣����������� | B�� | ���������⣬���Ǽ����� | ||
| C�� | ���Ǽ����⣬���������� | D�� | �٣��ڶ��Ǽ����� |
| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 9 |
| A�� | {3} | B�� | {1��2��4��5} | C�� | {1��2} | D�� | {1��3��5} |