题目内容
16.已知不等式组$\left\{\begin{array}{l}x-2y+1≥0\\ x≤3\\ x+y-1≥0\end{array}\right.$表示的平面区域为D,若函数y=|x-2|+m的图象上存在区域D上的点,则实数m的取值范围是( )| A. | [-3,1] | B. | $[-3,\frac{3}{2}]$ | C. | $[-1,\frac{3}{2}]$ | D. | [-1,1] |
分析 作出可行域,由y=|x-2|的图象特点,利用数形结合进行求解即可.
解答 解:作出不等式组表示的平面区域D(如图阴影),
函数y=|x-2|的图象
其图象为关于直线x=2对称的折线(图中红色虚线),
沿x=2上下平移y=|x-2|的图象,当经过点B时m取最小值,过点A时m取最大值,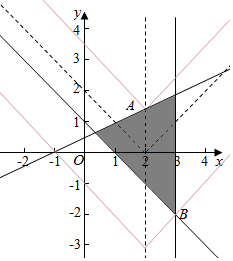
由$\left\{\begin{array}{l}{x=3}\\{x+y-1=0}\end{array}\right.$,可解$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$,即B(3,-2)此时有-2=|3-2|+m=1+m,解得m=-3;
由$\left\{\begin{array}{l}{x=2}\\{x-2y+1=0}\end{array}\right.$,可解得$\left\{\begin{array}{l}{x=2}\\{y=\frac{3}{2}}\end{array}\right.$,即A(2,$\frac{3}{2}$)此时有$\frac{3}{2}$=|2-2|+m=m,解得m=$\frac{3}{2}$;
故实数m的取值范围为$[-3,\frac{3}{2}]$,
故选:B.
点评 本题考查简单线性规划,利用绝对值函数的图象性质以及数形结合是解决问题的关键,属中档题.

练习册系列答案
相关题目
6.已知双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点为F,过F且斜率为$\sqrt{3}$的直线交C于A、B两点,若$\overrightarrow{AF}$=4$\overrightarrow{FB}$,则C的离心率为( )
| A. | $\frac{6}{5}$ | B. | $\frac{7}{5}$ | C. | $\frac{5}{8}$ | D. | $\frac{9}{5}$ |
4.若x,y满足约束条件$\left\{\begin{array}{l}{2x-y≥0}\\{x-y≤0}\\{x+y-3≥0}\\{\;}\end{array}\right.$,则z=2x+y的最小值是( )
| A. | 5 | B. | $\frac{9}{2}$ | C. | 4 | D. | $\frac{7}{2}$ |
8.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x+2y-3≤0}\\{x+3y-3≥0}\\{y-1≤0}\end{array}\right.$,若目标函数z=ax+y(其中a>0)仅在点(1,1)处取得最大值,则a的取值范围为( )
| A. | (0,2) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{3}$) | D. | ($\frac{1}{3},\frac{1}{2}$) |
6.设β=-123°-3×180°,则角β是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
