题目内容
8.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x+2y-3≤0}\\{x+3y-3≥0}\\{y-1≤0}\end{array}\right.$,若目标函数z=ax+y(其中a>0)仅在点(1,1)处取得最大值,则a的取值范围为( )| A. | (0,2) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{3}$) | D. | ($\frac{1}{3},\frac{1}{2}$) |
分析 由题意作平面区域,化目标函数z=ax+y为y=-ax+z,从而可得-$\frac{1}{2}$<-a<0,从而解得.
解答 解:由题意作平面区域如下,
化简z=ax+y得y=-ax+z,
结合图象可知,-$\frac{1}{2}$<-a<0,
解得,0<a<$\frac{1}{2}$,
故选:B.
点评 本题考查了线性规划问题,同时考查了数形结合的思想方法应用,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
18.某企业A向杜会迸行融资,先让个人B借给企业a万元(a>0),再从出借日的下个月开始,分成12个月,按月复利1%计算,每月企业等额返还给个人B,现企业A前6个月已按约定返还给个人B,由于某种特殊原因该融资必须停止,企业退还给B $\frac{a}{2}$万元,则该退还方式( )
| A. | 公平 | B. | 企业A吃亏 | C. | 个人B吃亏 | D. | 谁吃亏与a有关 |
16.已知不等式组$\left\{\begin{array}{l}x-2y+1≥0\\ x≤3\\ x+y-1≥0\end{array}\right.$表示的平面区域为D,若函数y=|x-2|+m的图象上存在区域D上的点,则实数m的取值范围是( )
| A. | [-3,1] | B. | $[-3,\frac{3}{2}]$ | C. | $[-1,\frac{3}{2}]$ | D. | [-1,1] |
20.“a=1”是“复数z=(a2-1)+2(a+1)i(a∈R)为纯虚数”的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
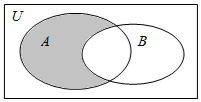 设全集U=R,A={x∈N|2x(x-4)<1},B={x∈N|y=ln(2-x)},则图中阴影部分表示的集合的子集个数为( )
设全集U=R,A={x∈N|2x(x-4)<1},B={x∈N|y=ln(2-x)},则图中阴影部分表示的集合的子集个数为( )