题目内容
11.已知命题p:“$?{x_0}∈R,|{x_0}|+x_0^2<0$”,则¬p为?x∈R,|x|+x2≥0.分析 直接利用特称命题的否定是全称命题写出结果即可.
解答 解:因为特称命题的否定是全称命题,所以命题p:“$?{x_0}∈R,|{x_0}|+x_0^2<0$”,则¬p为:?x∈R,|x|+x2≥0.
故答案为:?x∈R,|x|+x2≥0.
点评 本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.

练习册系列答案
相关题目
1.函数f(x)=($\frac{1}{2}$)x-x+2的零点所在的一个区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
2.某学校为了了解高一、高二、高三三个年级的学生的课外阅读时间是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是( )
| A. | 抽签法 | B. | 系统抽样法 | C. | 分层抽样法 | D. | 随机数法 |
16.已知不等式组$\left\{\begin{array}{l}x-2y+1≥0\\ x≤3\\ x+y-1≥0\end{array}\right.$表示的平面区域为D,若函数y=|x-2|+m的图象上存在区域D上的点,则实数m的取值范围是( )
| A. | [-3,1] | B. | $[-3,\frac{3}{2}]$ | C. | $[-1,\frac{3}{2}]$ | D. | [-1,1] |
20.“a=1”是“复数z=(a2-1)+2(a+1)i(a∈R)为纯虚数”的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
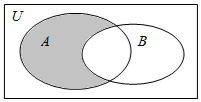 设全集U=R,A={x∈N|2x(x-4)<1},B={x∈N|y=ln(2-x)},则图中阴影部分表示的集合的子集个数为( )
设全集U=R,A={x∈N|2x(x-4)<1},B={x∈N|y=ln(2-x)},则图中阴影部分表示的集合的子集个数为( )