题目内容
6.已知双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点为F,过F且斜率为$\sqrt{3}$的直线交C于A、B两点,若$\overrightarrow{AF}$=4$\overrightarrow{FB}$,则C的离心率为( )| A. | $\frac{6}{5}$ | B. | $\frac{7}{5}$ | C. | $\frac{5}{8}$ | D. | $\frac{9}{5}$ |
分析 设AF=4m,BF=m.过A,B分别做准线的垂线,垂足为A1,B1.由双曲线定义得可分别表示出|AA1|和|BB1|,过B做BD垂直于AA1垂足D.根据直线的斜率可知∠ABD=30°进而求得|AD|和|AB|的关系求得e.
解答 解:设|AF|=4m,|BF|=m.
过A,B分别做准线的垂线,垂足为A1,B1.
由双曲线的第二定义得,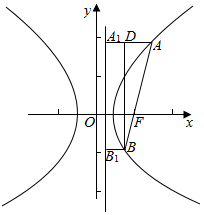
|AA1|=$\frac{4m}{e}$.|BB1|=$\frac{m}{e}$.过B做BD垂直于AA1垂足D.
在△ABD中,∠ABD=30°,|AD|=$\frac{1}{2}$|AB|.
即$\frac{3m}{e}$=$\frac{1}{2}$×5m.
解得e=$\frac{6}{5}$.
故选:A.
点评 本题主要考查了直线与圆锥曲线的综合问题,考查双曲线的离心率的求法,注意运用定义法,考查了学生综合分析问题和解决问题的能力,属于中档题.

练习册系列答案
相关题目
1.函数f(x)=($\frac{1}{2}$)x-x+2的零点所在的一个区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
18.某企业A向杜会迸行融资,先让个人B借给企业a万元(a>0),再从出借日的下个月开始,分成12个月,按月复利1%计算,每月企业等额返还给个人B,现企业A前6个月已按约定返还给个人B,由于某种特殊原因该融资必须停止,企业退还给B $\frac{a}{2}$万元,则该退还方式( )
| A. | 公平 | B. | 企业A吃亏 | C. | 个人B吃亏 | D. | 谁吃亏与a有关 |
15.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$$•\overrightarrow{a}$=$\overrightarrow{a}$$•\overrightarrow{b}$=$\overrightarrow{b}$$•\overrightarrow{c}$=1,$\overrightarrow{a}$$•\overrightarrow{c}$=2,则|$\overrightarrow{a}$$+\overrightarrow{b}$$+\overrightarrow{c}$|的取值范围为( )
| A. | [0,+∞) | B. | [2$\sqrt{2}$,+∞) | C. | [2$\sqrt{3}$,+∞) | D. | [4,+∞) |
16.已知不等式组$\left\{\begin{array}{l}x-2y+1≥0\\ x≤3\\ x+y-1≥0\end{array}\right.$表示的平面区域为D,若函数y=|x-2|+m的图象上存在区域D上的点,则实数m的取值范围是( )
| A. | [-3,1] | B. | $[-3,\frac{3}{2}]$ | C. | $[-1,\frac{3}{2}]$ | D. | [-1,1] |