题目内容
18.由一个长方体和两个$\frac{1}{4}$ 圆柱体构成的几何体的三视图如图,则该几何体的体积为2+$\frac{π}{2}$.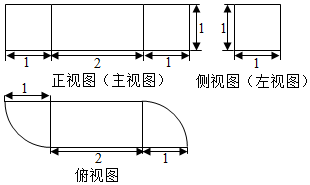
分析 由三视图可知:长方体长为2,宽为1,高为1,圆柱的底面半径为1,高为1圆柱的$\frac{1}{4}$,根据长方体及圆柱的体积公式,即可求得几何体的体积.
解答 解:由长方体长为2,宽为1,高为1,则长方体的体积V1=2×1×1=2,
圆柱的底面半径为1,高为1,则圆柱的体积V2=$\frac{1}{4}$×π×12×1=$\frac{π}{4}$,
则该几何体的体积V=V1+2V1=2+$\frac{π}{2}$,
故答案为:2+$\frac{π}{2}$.
点评 本题考查利用三视图求几何体的体积,考查长方体及圆柱的体积公式,考查计算能力,属于基础题.

练习册系列答案
相关题目
8.函数f(x)=ln(x2-2x-8)的单调递增区间是( )
| A. | (-∞,-2) | B. | (-∞,-1) | C. | (1,+∞) | D. | (4,+∞) |
6.若复数z满足z2=-4,则复数z的实部为( )
| A. | 2 | B. | 1 | C. | -2 | D. | 0 |

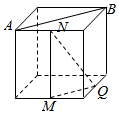
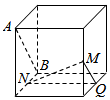
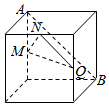
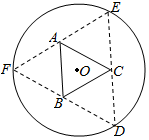 如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为4$\sqrt{15}$cm3.
如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为4$\sqrt{15}$cm3.