题目内容
已知函数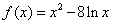 ,
,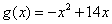 .
.
(1)求函数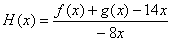 的单调递增区间;
的单调递增区间;
(2)若函数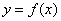 和函数
和函数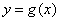 在区间
在区间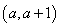 上均为增函数,求实数
上均为增函数,求实数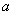 的取值范围;
的取值范围;
(3)若方程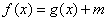 有两个解,求实数
有两个解,求实数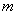 的取值范围.
的取值范围.
(1)解:∵  (
( ∴
∴ 令
令 ,得
,得
故函数 的单调递增区间为
的单调递增区间为 ……………………………………4分
……………………………………4分
(2)
 当
当 时,
时, ,当
,当 时,
时, ,要使
,要使 在
在 上递增,必须
上递增,必须
 ,如使
,如使 在
在 上递增,必须
上递增,必须 ,即
,即 ,由上得出,当
,由上得出,当 时
时 ,
, 在
在 上均为增函数 ……9分
上均为增函数 ……9分
(3)方程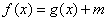 有两个解
有两个解 有两个解
有两个解
设 ,
, (
( )
)
 随
随 变化如下表
变化如下表
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
由于在 上,
上, 只有一个极小值,
只有一个极小值,
 的最小值为
的最小值为 ,
,
当m
 时,方程
时,方程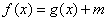 有两个解. ……………14分
有两个解. ……………14分

练习册系列答案
相关题目








 ,则“
,则“ 且
且 ”是“点
”是“点 在直线
在直线 上”的 ( )
上”的 ( )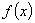 满足
满足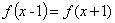 ,且在
,且在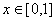 时,
时, 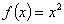 ,
,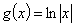 ,
,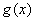 图象交点的个数是 .
图象交点的个数是 . ,则目标函数
,则目标函数 的取值范围是( )
的取值范围是( )  ,2] D.[2,6]
,2] D.[2,6] =(3,-4),
=(3,-4), =(6,-3),
=(6,-3), =(5-m,-3-m).若∠ABC为锐角,则实数m的取值范围 .
=(5-m,-3-m).若∠ABC为锐角,则实数m的取值范围 . 与直线
与直线 没有公共点的充要条件是( )
没有公共点的充要条件是( ) B.
B.
 D.
D.
 可能取的值为1,2,3,4;
可能取的值为1,2,3,4; (
( 1,2,3,4).
1,2,3,4). .
.
 }中,已知
}中,已知
 ,则n为 ( )
,则n为 ( )