题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c.已知 =
= .
.
(1)求 的值;
的值;
(2)若cos B= ,△ABC的周长为5,求b的长.
,△ABC的周长为5,求b的长.
解析 (1)由正弦定理,设 =
= =
= =k,
=k,
则 =
= =
= ,
,
所以 =
= .
.
即(cos A-2cos C)sin B=(2sin C-sin A)cos B,
化简可得sin(A+B)=2sin(B+C).
又A+B+C=π,
所以sin C=2sin A,因此 =2.
=2.
(2)由 =2得c=2a.
=2得c=2a.
由余弦定理及cos B= 得
得
b2=a2+c2-2accos B=a2+4a2-4a2× =4a2.
=4a2.
所以b=2a.又a+b+c=5.从而a=1,因此b=2.

练习册系列答案
相关题目
 +sin α
+sin α =________.
=________. ,cos x=
,cos x=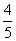 ,则tan 2x等于( ).
,则tan 2x等于( ). B.-
B.- D.-
D.-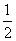 B.
B. BC,则S△ABC的最大值________.
BC,则S△ABC的最大值________.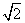 a km
a km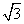 a km
a km
 =
=
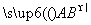 ,DE∥BC交AC于E,AM是BC边上的中线,交DE于N.设
,DE∥BC交AC于E,AM是BC边上的中线,交DE于N.设 =b,用a,b分别表示向量
=b,用a,b分别表示向量 ,
, ,
, ,
, ,
, ,
, .
. 
 |b|,若函数f(x)=
|b|,若函数f(x)= x3+|a|x2+2a·bx+1在x∈R上有极值,则〈a,b〉的取值范围是( )
x3+|a|x2+2a·bx+1在x∈R上有极值,则〈a,b〉的取值范围是( ) 